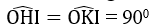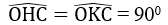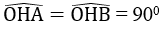Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

Bài 24 trang 160 Sách bài tập Toán 9 Tập 1:

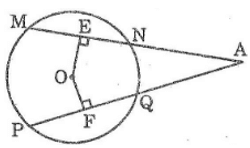
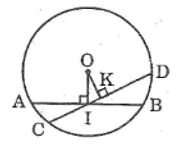
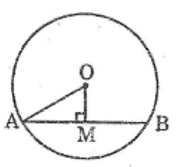
 Cho hình bên, trong đó MN = PQ. Chứng minh rằng:

a. AE = AF    b. AN = AQ

Lời giải:

a. Nối OA

Ta có: MN = PQ (gt)

Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)

Xét hai tam giác OAE và OAF, ta có:

OA chung

OE = OF (chứng minh trên)

Suy ra: ∆OAE = ∆OAF (cạnh huyền, cạnh góc vuông)

Suy ra: AE = AF

b. Ta có: OE ⊥ MN (gt)

Suy ra EN = (1/2).MN (đường kính vuông góc với dây cung)     (1)

OF ⊥ PQ (gt)

Suy ra FQ = (1/2).PQ (đường kính vuông góc với dây cung)     (2)

Mặt khác: MN = PQ (gt)     (3)

Từ (1), (2) và (3) suy ra: EN = FQ     (4)

Mà AE = QF (chứng minh trên)     (5)

Từ (4) và (5) suy ra: AN + NE = AQ + QF     (6)

Từ (5) và (6) suy ra: AN = AQ

 

Bài 25 trang 160 Sách bài tập Toán 9 Tập 1: 

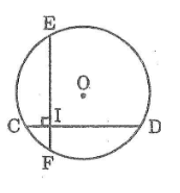
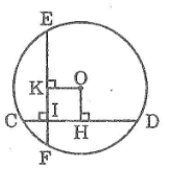
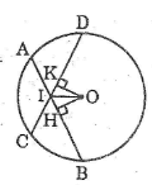
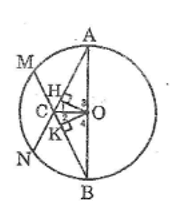
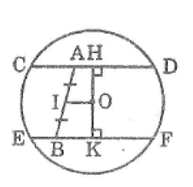
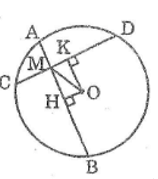
Cho hình bên, trong đó có hai dây CD, EF bằng nhau và vuông góc với nhau tại I, IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến mỗi dây

Lời giải:

Kẻ OH ⊥ CD, OK ⊥ EF

Vì tứ giác OKIH có ba góc vuông nên nó là hình chữ nhật.

Ta có: CD = EF (gt)

Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)v

Suy ra tứ giác OKIH là hình vuông.

Ta có:

CD = CI + ID = 2 + 14 = 16(cm)

HC = HD = CD/2 = 8 (cm) (đường kính dây cung)

IH = HC – CI = 8 – 2 = 6 (cm)

Suy ra: OH = OK = 6 (cm) (OKIH là hình vuông)

 

Bài 26 trang 160 Sách bài tập Toán 9 Tập 1: 

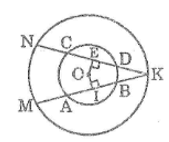
Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O; OK) cắt KA và KC tại M và N. Chứng minh rằng KM < KN.

Lời giải:

Kẻ OI ⊥ AB, OE ⊥ CD

Trong (O; OA) ta có: AB < CD (gt)

Suy ra : OI > OE (dây lớn hơn gần tâm hơn)

Trong (O ; OK) ta có : OI > OE (cmt)

Suy ra : KM < KN (dây gần tâm hơn thì lớn hơn)

 

Bài 27 trang 160 Sách bài tập Toán 9 Tập 1: 

Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với IO tại I ngắn hơn mọi dây khác đi qua I.

Lời giải:

Gọi CD là dây bất kì đi qua I và CD không vuông góc với OI.

Kẻ OK ⊥ CD

Tam giác OKI vuông tại K nên OI > OK

Suy ra : AB < CD (dây lớn hơn gần tâm hơn)

Vậy dây AB vuông góc với IO tại I ngắn hơn mọi dây khác đi qua I.

 

Bài 28 trang 160 Sách bài tập Toán 9 Tập 1:

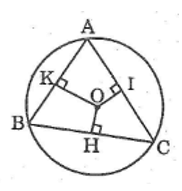
 Tam giác ABC nội tiếp đường tròn (O) có 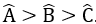 . Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK.

Lời giải:

Tam giác ABC có 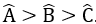 nên suy ra :

BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)

Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)

Mà BC > AC > AB nên suy ra:

OH < OI < OK (dây lớn hơn gần tâm hơn)

Bài 29 trang 161 Sách bài tập Toán 9 Tập 1:

 Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:

a. OI là tia phân giác của một trong hai góc tạo bởi hai dây AB, CD.

b. Điểm I chia AB, CD thành các đoạn thẳng bằng nhau đôi một.

Lời giải:

a. Kẻ OH ⊥ AB, OK ⊥ CD

Ta có: AB = CD (gt)

Suy ra : OH = OK (hai dây bằng nhau cách đều tâm)

Vậy OI là tia phân giác của góc BID (tính chất đường phân giác)

b. Xét hai tam giác OIH và OIK, ta có :

OI chung

OH = OK (chứng minh trên)

Suy ra: ∆OIH = ∆OIK (cạnh huyền, cạnh góc vuông)

Suy ra: IH = IK     (1)

Lại có: HA = HB = (1/2).AB

KC = KD = (1/2).CD

Mà AB = CD nên HA = KC     (2)

Từ (1) và (2) suy ra: IA = IC

Mà AB = CD nên IB = ID

 

Bài 30 trang 161 Sách bài tập Toán 9 Tập 1: 

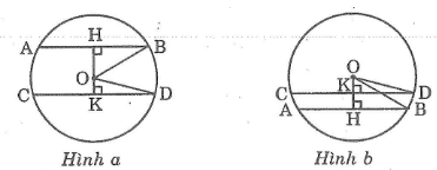
Cho đường tròn tâm O bán kính 25cm. Hai dây AB, CD song song với nhau và có độ dài theo thứ tự bằng 40cm, 48cm. Tính khoảng cách giữa hai dây ấy.

Lời giải:

Kẻ OK ⊥ CD ⇒ CK = DK = (1/2).CD

Kẻ OH ⊥ AB ⇒ AH = BH = (1/2).AB

Vì AB // CD nên H, O, K thẳng hàng

Áp dụng định lí Pitago vào tam giác vuông OBH ta có:

OB² = BH² + OH²

Suy ra: OH² = OB² – BH² = 25² – 20²= 225

OH = 15 (cm)

Áp dụng định lí Pitago vào tam giác vuông ODK ta có:

OD² = DK² + OD²

Suy ra: OK² = OD² – DK² = 25² – 24² = 49

OK = 7 (cm)

* Trường hợp O nằm giữa hai dây AB và CD (hình a):

HK = OH + OK = 15 + 7 = 22 (cm)

* Trường hợp O nằm ngoài hai dây AB và CD (hình b):

HK = OH – OK = 15 – 7 = 8 (cm)

 

Bài 31 trang 161 Sách bài tập Toán 9 Tập 1: 

Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:

a. OC là tia phân giác của góc AOB

b. OC vuông góc với AB

Lời giải:

a. Kẻ OH ⊥ AM, OK ⊥ AN

Ta có: AM = AN (gt)

Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)

Xét hai tam giác OCH và OCK, ta có:

OC chung

OH = OK (chứng minh trên)

Suy ra: ∆OIH = ∆OIK (cạnh huyền, cạnh góc vuông)

Xét hai tam giác OAH và OBH, ta có:

OA = OB

OH = OK (chứng minh trên)

Suy ra: ∆OAH = ∆OBH (cạnh huyền, cạnh góc vuông)

b. Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao (tính chất tam giác cân)

Suy ra: OC ⊥ AB

Bài 32 trang 161 Sách bài tập Toán 9 Tập 1: 

Cho đường tròn tâm O bán kính 5dm, điểm M cách O là 3dm

a. Tính độ dài dây ngắn nhất đi qua M.

b. Tính độ dài dây dài nhất đi qua M

Lời giải:

a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM

Áp dụng định lí Pitago vào tam giác vuông OAM ta có:

OA² = AM² + OM²

Suy ra: AM² = OA² – OM² = 5² – 3² = 16

AM = 4 (dm)

Ta có: OM ⊥ AB

Suy ra: AM = (1/2).AB

Hay: AB = 2AM = 2.4 = 8 (dm)

b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

Bài 34 trang 161 Sách bài tập Toán 9 Tập 1: 

Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại

Lời giải:

* Cách dựng

– Dựng trung điểm I của AB

– Qua A dựng dây CD song song với OI

– Qua B dựng dây EF song song với OI

Ta được CD và EF là hai dây cần dựng

* Chứng minh

Ta có : CD // OI, EF // OI

Suy ra : CD // EF

Kẻ OH ⊥ CD cắt EF tại K

Suy ra: OK ⊥ EF

Lại có: IA = IB

Suy ra: OH = OK

Vậy CD = EF.