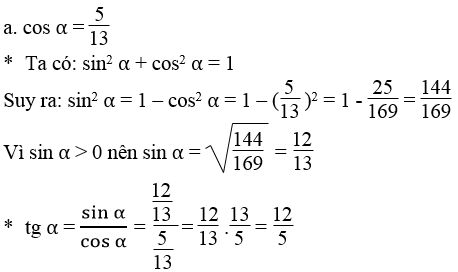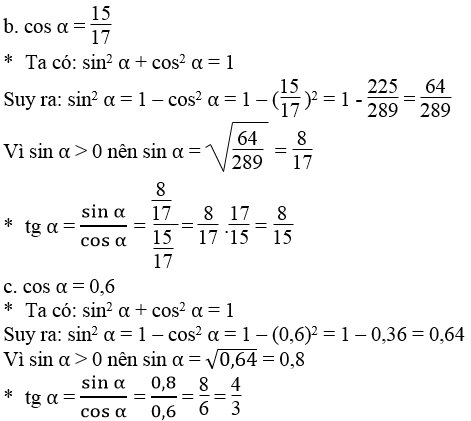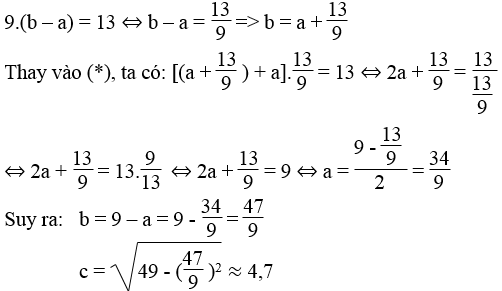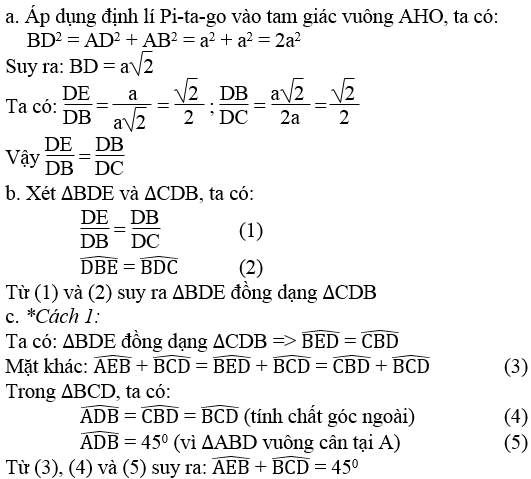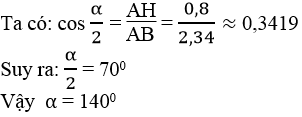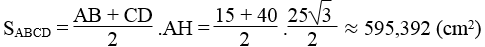Ôn tập chương I

Bài 80 trang 119 Sách bài tập Toán 9 Tập 1:

Hãy tính sin α và tg α nếu:

a. cos α = 5/13     b. cos α = 15/17     c. cos α = 0,6

Lời giải:

 

Bài 81 trang 119 Sách bài tập Toán 9 Tập 1:

Hãy đơn giản các biểu thức:

a. 1 – sin²α     b. (1 – cos α)(1 + cos α)

c. 1 + sin²α + cos²α     d. sin α – sin α cos²α

e. sin⁴α + cos⁴α + 2sin²α cos²α     g. tg²α – sin²α tg²α

h. cos²α + tg²α cos²α     i. tg²α.(2cos²α + sin²α – 1)

Lời giải:

a. 1 – sin²α = (sin²α + cos²α) – sin²α

= sin²α + cos²α – sin²α = cos²α

b. (1 – cos α)(1 + cos α) = 1 – cos²α = (sin²α + cos²α) – cos²α

= sin²α + cos²α – cos²α = sin²α

c. 1 + sin²α + cos²α = 1 + (sin²α + cos²α) = 1 + 1 = 2

d. sin α – sin α cos²α = sin α(1 – cos²α)

= sin α[(sin²α + cos²α) – cos²α]

= sin α.(sin²α + cos²α – cos²α)

= sin α.sin²α = sin³α

e. sin⁴α + cos⁴ + 2sin²α cos²α = (sin²α + cos²α)²α = 12 = 1

g. tg²α – sin²α tg²α = tg²α (1 – sin²α)

= tg²α [(sin²α + cos²α) – sin²α]

= tg²α.cos²α = (sin²α)/(cos²α) .cos²α = sin²α

h. cos²α + tg²α cos²α = cos²α + (sin²α)/(cos²α) .cos²α = cos²α + sin²α = 1

i. tg²α.(2cos²α + sin²α – 1) = tg²α.[cos²α + (cos²α + sin²α) – 1]

= tg²α.(cos²α + 1 – 1) = tg²α.cos²α

= (sin²α)/(cos²α) .cos²α = sin²α

 

Bài 82 trang 120 Sách bài tập Toán 9 Tập 1:

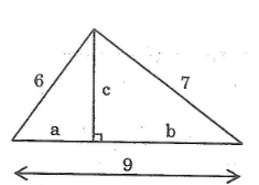
 Trong một tam giác với các cạnh có độ dài 6, 7, 9, kẻ đường cao đến cạnh lớn nhất. Hãy tìm độ dài đường cao này và các đoạn thẳng mà nó định ra trên cạnh lớn nhất đó.

Lời giải:

Gọi độ dài đường cao là c, hình chiếu của hai cạnh 6 và 7 trên cạnh có độ dài bằng 9 lần lượt là a và b.

Ta có: a < b (vì 6 < 7)

Theo định lí Pi-ta-go, ta có:

c² = 6² – a²

c² = 7² – b²

Suy ra: 36 – a² = 49 – b²

⇔ b² – a² = 49 – 36

⇔ (b + a)(b – a) = 13 (*)

Mà x + y = 9 nên:

 

Bài 83 trang 120 Sách bài tập Toán 9 Tập 1:

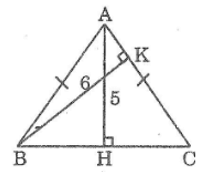
 Hãy tìm độ dài cạnh đáy của một tam giác cân, nếu đường cao kẻ xuống đáy có độ dài là 5 và đường cao kẻ xuống cạnh bên có độ dài là 6.

Lời giải:

Bài 84 trang 120 Sách bài tập Toán 9 Tập 1:

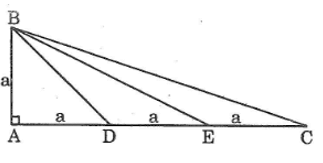
Tam giác ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC

a. Chứng minh DE/DB = DB/DC

b. Chứng minh tam giác BDE đồng dạng tam giác CDB

c. Tính tổng 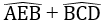 bằng 2 cách:

Cách 1: Sử dụng kết quả ở câu b

Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.

Lời giải:

 

Bài 85 trang 120 Sách bài tập Toán 9 Tập 1:

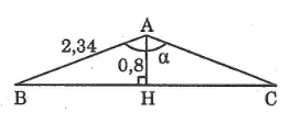
Tính góc α tạo bởi hai mái nhà, biết rằng mỗi mái nhà dài 2,34m và cao 0,8m

Lời giải:

Hai mái nhà bằng nhau tạo thành hai cạnh của một tam giác cân. Chiều cao của mái nhà chia góc ở đỉnh ra thành hai phần bằng nhau.

 

Bài 86 trang 120 Sách bài tập Toán 9 Tập 1:

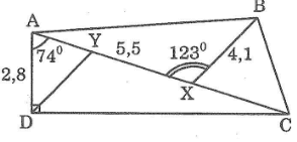
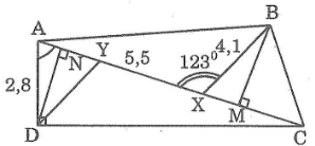
 Cho hình bên.

Biết AD ⊥ DC,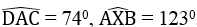 , AD = 2,8cm, AX = 5,5cm, BX = 4,1cm.

a. Tính AC

b. Gọi Y là điểm trên AX sao cho DY // BX. Hãy tính XY

c. Tính diện tích tam giác BCX

Lời giải:

 

 

Bài 87 trang 120 Sách bài tập Toán 9 Tập 1: 

Tam giác ABC có 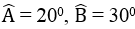 , AB = 60cm. Đường vuông góc kẻ từ C đến AB cắt AB tại P. Hãy tìm:

a. CP     b. AP, BP

Lời giải:

b. Thay CP = 13,394 vào (1) ta có:

AP = 13,394.cotg20^o ≈ 36,801 (cm)

Thay CP = 13,394 vào (2) ta có:

BP = 13,394.cotg30^o ≈ 27,526 (cm)

 

 

Bài 88 trang 121 Sách bài tập Toán 9 Tập 1: 

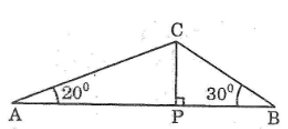
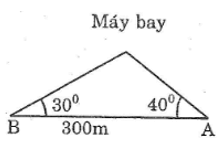
Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc “nâng” để nhìn thấy máy bay tại vị trí A là 40^o và tại vị trí B là 30^o (hình bên). Hãy tìm độ cao của máy bay.

Lời giải:

Gọi C là vị trí của máy bay.

Kẻ CH ⊥ AB

Trong tam giác vuông ACH, ta có:

AH = CH.cotg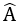 (1)

Trong tam giác vuông BCH, ta có:

BH = CH.cotg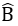 (2)

Từ (1) và (2) suy ra: (AH + BH) = CH.cotg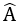 + CH.cotg

Suy ra: CH = 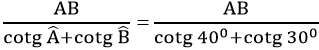 ≈ 102,606 (cm)

 

 

Bài 89 trang 121 Sách bài tập Toán 9 Tập 1:

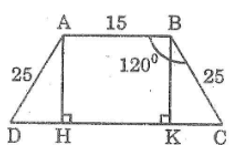
Cho hình thang với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm, góc tù bằng 120^o. Tính chu vi và diện tích hình thang đó.

Lời giải:

Giả sử hình thang ABCD có đáy nhỏ AB = 15cm, cạnh bên AD = BC = 25cm,

Mà ∆ADH = ∆BCK (cạnh huyền, cạnh góc vuông)

Suy ra: DH = CK = 12,5 (cm)

Chu vi hình thang ABCD là:

AB + BC + CD + DA = AB + BC + (CK + KH + HD) + DA

= 15 + 25 + (12,5 + 15 + 12,5) + 25 = 105 (cm)

Chu vi hình thang ABCD là: