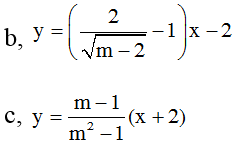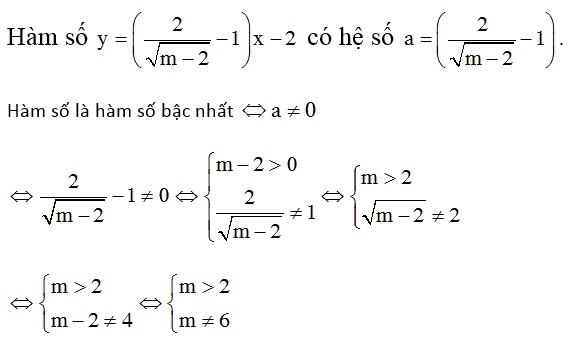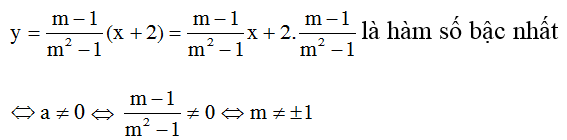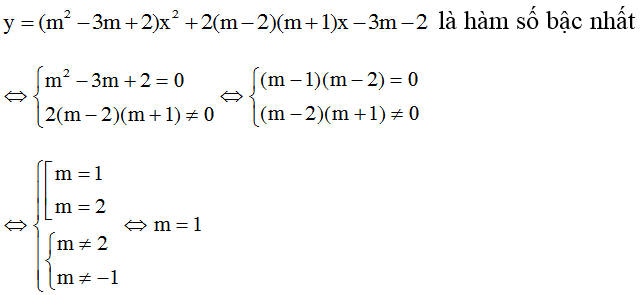Tìm điều kiện để hàm số là hàm bậc nhất. Hàm số đồng biến, nghịch biến

A. Phương pháp giải

Hàm số y=ax+b là hàm số bậc nhất ⇔ a ≠ 0.

Hàm số y=ax+b (với a ≠ 0)

+ Đồng biên trên R, khi a > 0.

+ Nghịch biến trên R, khi a < 0.

B. Bài tập tự luận

Bài 1:

Tìm k để các hàm số sau:

a, y= 5x – (2-x)k đồng biến, nghịch biến.

b, y= (k² – 4)x – 2 đồng biến.

c, y= (-k² + k – 1)x – 7 nghịch biến.

d, y= (4 – 4k + k²)x + 2 đồng biến.

Hướng dẫn giải

a, y= 5x – (2-x)k = 5x – 2k + k.x = (5+k)x – 2k

Vậy hàm số có hệ số a= 5+k. Khi đó:

+ Hàm số đồng biến a > 0 ⇔ 5 + k > 0 ⇔ k > -5

+ Hàm số nghịch biến a < 0 ⇔ 5 + k < 0 ⇔ k < -5.

Bài 2: Với những giá trị nào của m thì hàm số sau là hàm số bậc nhất?

a, y= mx – 2(x-m)

d, y= (m² – 3m + 2)x² + 2(m-2)(m+1)x – 3m – 2.

Hướng dẫn giải

a) Hàm số y = mx – 2(x-m) = (m-2)x + 2m có hệ số a=m-2.

Vậy hàm số y = mx – 2(x-m) là hàm số bậc nhất ⇔ a ≠ 0 ⇔ m – 2 ≠ 0 ⇔ m ≠ 2.

b)

Vậy m > 2 và m ≠ 6.

c)

Vậy m ≠ ± 1

d)

Vậy m = 1

Bài 3:

Cho hàm số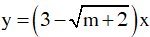.Với gía trị nào của m thì :

a, Hàm số đã cho là hàm bậc nhất

b, Hàm số đã cho đồng biến

c, Hàm số đã cho nghịch biến

Hướng dẫn giải

Hàm số đã cho có hệ số a= 3 – √(m+2).

a, Hàm số đã cho là hàm bậc nhất ⇔ a ≠ 0 ⇔ 3 – √(m+2) ≠ 0 ⇔ √(m+2) ≠ 3

⇔ m + 2 ≠ 9 ⇔ m ≠ 7

Vậy m ≠ 7

b, Hàm số đã cho đồng biến khi a > 0 ↔ 3 – √(m+2) > 0 ⇔ √(m+2) < 3

⇔ 0 ≤ m + 2 < 9 ⇔ -2 ≤ m < 7

Vậy -2 ≤ m < 7

c, Hàm số đã cho nghịch biến khi a < 0 3 – √(m+2) < 0 ⇔ √(m+2) > 3

⇔ m + 2 >; 9 ⇔ m > 7

Vậy m > 7