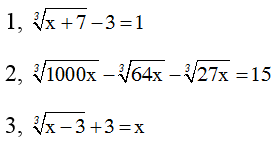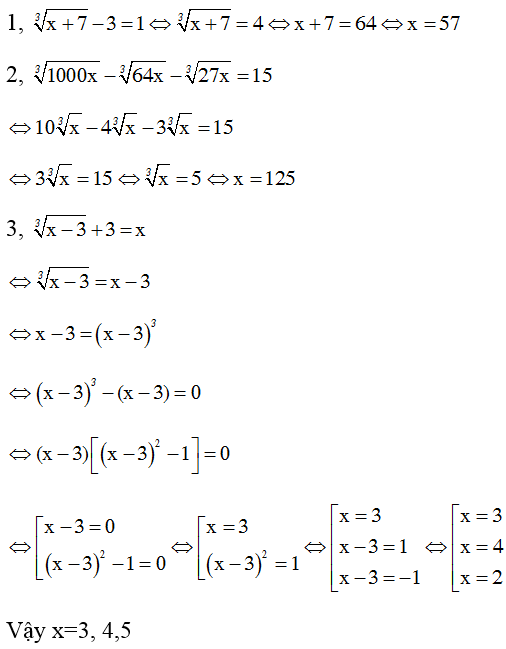Căn bậc ba

A. Phương pháp giải

1, Khái niệm căn bậc ba Căn bậc ba của một số a là số x sao cho x³ = a.

∛a = x ⇔ x³ = a Như vậy, (∛a)³ = ∛(a³) = a Nhận xét: – Căn bậc ba của số dương là số dương. – Căn bậc ba của số âm là số âm. – Căn bậc ba của số 0 là số 0. 2, Tính chất 1, a < b ⇔ ∛a < ∛b 2, ∛(ab) = ∛a . ∛b 3, ∛(a/b) = ∛a / ∛b

B. Bài tập tự luận

Bài 1:

Tìm căn bậc ba của một số

A. Phương pháp giải

Dựa vào định nghĩa căn bậc ba của một số: ∛a³ = a

Tính căn bậc ba của các số sau

1. ∛216

2. ∛729

3. ∛-343

4. ∛-1000

5. ∛8/27

6. ∛(-125/512)

Hướng dẫn giải

1. ∛216 = 6

2. ∛729 = 9

3. ∛-343 = -7

4. ∛-1000 = -10

5. ∛8/27 = 2/3

6. ∛(-125/512) = -5/8

Bài 2:

A. Phương pháp giải

Đưa thừa số vào trong dấu căn: a∛b = ∛a³b

So sánh hai số trong dấu căn a < b ⇔ ∛a < ∛b

So sánh hai số sau

1. 7 và ∛345

2. 2∛6 và 3∛2

3. 2/3∛18 và 3/4∛12

Hướng dẫn giải

1. Ta có 7 = ∛343 < ∛345

2. Ta có 2∛6 = ∛48

3∛2 = ∛54

Vì 48 < 54 nên 2∛6 < 3∛2

3. 2/3∛18 = ∛16/3

3/4∛12 = ∛81/16

Vì 16/3 > 81/16 nên 2/3∛18 > 3/4∛12

Bài 3:

Thực hiện các phép tính:

1. ∛8 + ∛-27 + ∛-64

2. ∛54 – ∛-16 + ∛128

3. ∛16.∛13,5 – ∛120: ∛15

Hướng dẫn giải

1. ∛8 + ∛-27 + ∛-64 = 2 +(-3) + (-4) = -5

2. ∛54 – ∛-16 + ∛128 = 3∛2 + 2∛2 + 4∛2 = 9∛2

3. ∛16.∛13,5 – ∛120: ∛15 = ∛216 – ∛8 = 6 – 2 = 4

Bài 4:

A. Phương pháp giải

– Nếu x³ = a thì x = ∛a

– Nếu ∛x = b thì x = b³

Giải các phương trình sau:

Hướng dẫn giải