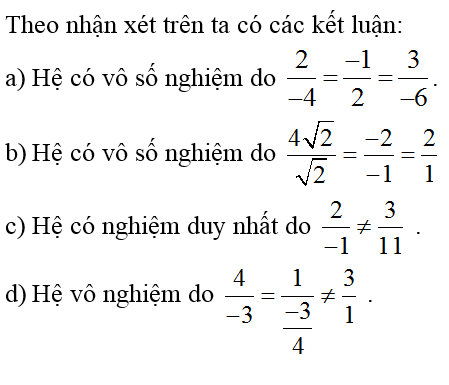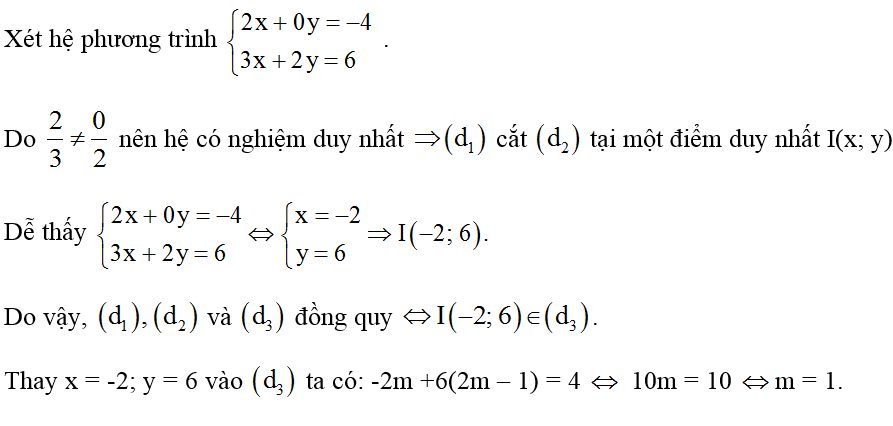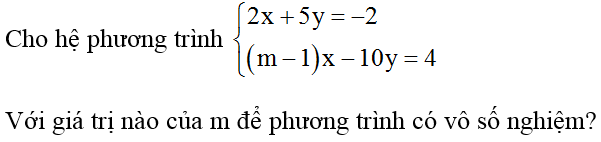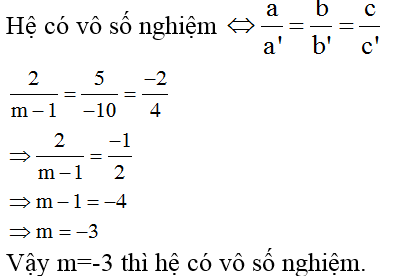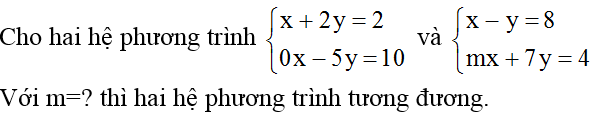Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn
A. Phương pháp giải
1. Khái niệm về hệ hai phương trình bậc nhất hai ẩn
Trong đó a, b, c, a’, b’, c’ là các số cho trước, x và y gọi là ẩn số.
Nếu hai phương trình (1) và (2) có nghiệm chung thì gọi là nghiệm của hệ phương trình. Hệ phương trình vô nghiệm nếu hai phương trình (1) và (2) không có nghiệm chung.
Giải hệ phương trình là tìm tất cả các nghiệm của nó.
Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm (có thể cùng vô nghiệm).
2. Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn
B. Bài tập tự luận
Bài 1:
Dựa vào các hệ số a, b, c, a’, b’, c; dự đoán số nghiệm của các phương trình sau:
Hướng dẫn giải
Bài 2:
Tìm m để các đường thẳng sau đồng quy:
(d1): 2x + 0y = -4
(d2): 3x + 2y = 6
(d3): mx + (2m – 1)y = 4
Hướng dẫn giải
Bài 3:
Hướng dẫn giải
Bài 4:
Hướng dẫn giải
Bài 5:
Hướng dẫn giải
Bài 6:
Cho phương trình: 3x – 4y = 5.
Hãy viết thêm một phương trình bậc nhất hai ẩn để có được một hệ phương trình:
a) Có nghiệm duy nhất.
b) Vô nghiệm.
c) Có vô số nghiệm.
Hướng dẫn giải
a) Để hệ có nghiệm duy nhất thì 3/a ≠ -4/b => 3b ≠ -4a
Ví dụ phương trình cần tìm là 3x + 5y = 1
b) Để hệ vô nghiệm thì 3/a = -4/b ≠ 5/c
Ví dụ lấy a=3; b=-4; c=10. Khi đó ta được phương trình 3x – 4y = 10
c) Để hệ có vô số nghiệm thì 3/a = -4/b = 5/c
Ví dụ lấy a = 6; b = -8; c = 10 ta được phương trình 6x – 8y = 10