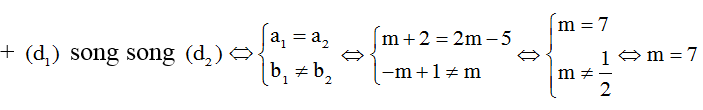Đường thẳng song song và đường thẳng cắt nhau. Tìm tọa độ giao điểm

A. Phương pháp giải

1. Với hai đường thẳng y=ax+b (d) và y=a’x + b’ ( trong đó a và a’ khác 0), ta có:

+ (d) và (d’) cắt nhau ⇔ a ≠ a’.

+ (d) và (d’) song song với nhau ⇔ a = a’ và b = b’.

+ (d) và (d’) trùng nhau ⇔ a = a’ và b = b’

+ (d) và (d’) vuông góc với nhau ⇔ a.a’= 1

2. Tọa độ giao điểm của (d) và (d’) là nghiệm của hệ phương trình:

y= ax + b.

y= ax’ + b’.

+ Điểm A(x_A; y_A) ∈ (d) ⇔ Tọa độ điểm A nghiệm đúng phương trình của (d).

B. Bài tập tự luận

Bài 1:

Tìm m để hai đường thẳng song song hoặc trùng nhau:

a, (d1): y= (m+2)x – m + 1 và (d2): y= (2m-5)x +m.

b, (d1): y= (3m-1)x – 2m + 1 và (d2): y= (4-2m)x -m.

Hướng dẫn giải

a) (d1): y = (m+2)x – m + 1 có hệ số a1 = m+2, b1 = -m +1

(d2): y = (2m-5)x + m có hệ số a2 = 2m – 5, b2 = m

Vậy khi m = 7 thì (d1) song song với (d2)

Bài 2:

Cho đường thẳng (AB): y = -1/3x + 2/3; (BC): y = 5x+1; (CA): y = 3x. Xác định tọa độ ba đỉnh của tam giác ABC

Hướng dẫn giải

Điểm B là giao điểm của (AB) và (BC):

Phương trình hoành độ giao điểm B:

-1/3x + 2/3 = 5x +1

⇔ 5x + 1/3 = 2/3 -1

⇔ x.16/3 = -1/3

⇔ x = -1/16

=> y = -1/3. -1/16 +2/3 = 11/16

Vậy B(-1/16;11/16)

Điểm A là giao điểm của (AB) và (AC) nên:

Phương trình hoành độ giao điểm A:

-1/3x + 2/3 = 3x

⇔ 3x + 1/3x = 2/3

⇔ x.10/3 = 2/3

⇔ x = 1/5

=> y = 3.1/5 = 3/5

Vậy A(1/5;3/5)

Điểm C là giao điểm của (BC) và (AC) nên:

Phương trình hoành độ giao điểm C:

5x + 1 = 3x

⇔ 2x = -1

⇔ x = -1/2

> y = 3.(-1/2) = -3/2

Vậy C(-1/2;-3/2)

Bài 3:

Cho đường thẳng (d) có dạng: y= (m+1)x -2m. Tìm m để:

a, Đường thẳng (d) đi qua điểm A(3;-1)

b, Đường thẳng (d) cắt trục hoành tại điểm có hoành độ là -1

c, Đường thẳng (d) song song với đường thẳng (d’): y=-2x+2

d, Đường thẳng (d) vuông góc với đường thẳng y= -3x-1

e, Đường thẳng (d) có hệ số góc là 3

f, Đường thẳng (d) có tung độ gốc là √2

g, Đường thẳng (d) có góc tạo bởi đường thẳng (d) và trục Ox là góc tù

Hướng dẫn giải

a, Cho (d): y= (m+1)x -2m.

Điểm A(3;-1) thuộc (d) ⇔ -1 = (m+1).3 – 2m

⇔ -1 = 3m + 3 – 2m.

⇔ m = 4

Vậy m = 4.

b, Tọa độ giao điểm của (d) với trục hoành là I(-1;0)

0 = (m+1)(-1) – 2m.

⇔ 0 = -m – 1 – 2m ⇔ 3m = -1 ⇔ m = -1/3

Vậy m= -1/3

c, (d) song song với (d’): y=-2x+2

⇔ m + 1 = -2 và -2m ≠ 2

⇔ m = -3 và m ≠ -1

⇔ m = -3

Vậy m = -3

d, Đường thẳng (d) vuông góc với đường thẳng: y=-3x-1

⇔ (m+1)(-3) = -1 ⇔ m + 1 = 1/3 ⇔ m = -2/3

Vậy m = -2/3

e, Đường thẳng (d) có hệ số góc là 3 ⇔ m + 1 = 3 ⇔ m = 2

f, Đường thẳng (d) có tung độ gốc là √2, tức là (d) đi qua điểm B(0, √2)

⇔ -2m = √2 ⇔ m = -√/2

g, Góc tạo bởi đường thẳng (d) và trục Ox là góc tù:

⇔ m + 1 < 0 ⇔ m < -1

Vậy m < -1.

Bài 4:

Tìm m để ba đường thẳng sau đồng quy.

(d1): y= (m+2)x – 3m

(d2): y= 2x + 4

(d3): y= -3x – 1

Hướng dẫn giải

Gọi A là giao điểm của (d2) và (d3):

Phương trình hoành độ giao điểm A:

2x + 4 = -3x – 1

⇔ 5x = -5

⇔ x = -1

=> y = 2(-1) + 4 = 2

=> A(-1;2)

Để (d1);(d2);(d3) đồng quy thì A(-1;2) ∈ (d1)

⇔ 2 = (m+2).(-1) – 3m

⇔ 2 = -2 – 4m

⇔ 4m = 4

⇔ m = -1

Vậy khi m = -1 thì (d1);(d2);(d3) đồng quy tại A(-1;2).