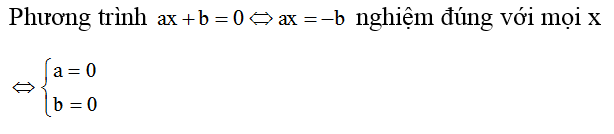Chứng minh đồ thị hàm số luôn đi qua một điểm cố định

A. Phương pháp giải

B. Bài tập tự luận

Bài 1:

Chứng minh các đường thẳng có phương trình sau luôn đi qua 1 điểm cố định.

a, y = 3(m + 1)x – 3m – 2

b, (m + 2)x + (m-3)y – m + 8 = 0

Hướng dẫn giải

a, y = 3(m + 1)x – 3m – 2

Giả sử đồ thị hàm số đi qua điểm M(x_o;y_o) với mọi m

Ta có: y_o = 3(m+1)x_o – 3m – 2

⇔ y_o = 3x_om + 3x_o – 3m – 2

⇔ (3x_o -3)m = y_o – 3x_o + 2

⇔ 3x_o – 3 = 0 và y_o – 3x_o + 2 = 0

⇔ x_o = 1; y_o = 1

b, (m + 2)x + (m-3)y – m + 8 = 0

Giả sử đồ thị hàm số đi qua điểm M(x_o; y_o) với mọi m

Ta có: (m+2)x_o + (m-3)y_o – m + 8 = 0

⇔ mx_o + 2x_o + my_o – m + 8 = 0

⇔ m(x_o + y_o -1) + 2x_o – 3y_o + 8 = 0

⇔ x_o + y_o – 1 = 0 và -2x_o + 3y_o – 8 = 0

⇔ x_o = -1 và y_o = 2

Bài 2:

Cho đường thẳng (d) có dạng: y=(2a-1)x-3.

a, Viết phương trình đường thẳng (d) biết đường thẳng đi qua A(1;-1)

b, Viết phương trình đường thẳng (d’) vuông góc với đường thẳng (d) và cắt trục tung tại B có tung độ là 4/3 .

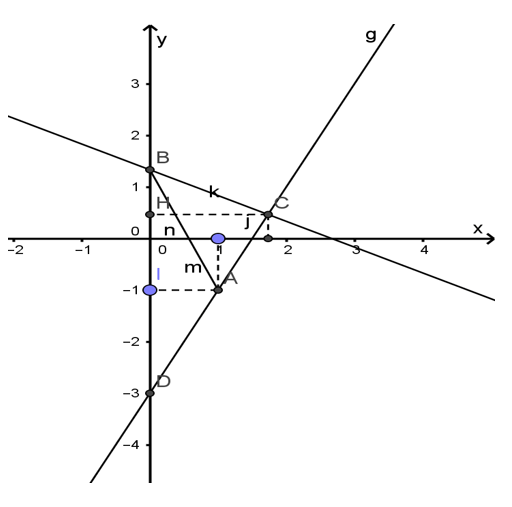
c, Vẽ (d) và (d’) trên cùng một mặt phẳng tọa độ. Tìm giao điểm C giữa (d) và (d’).

Hướng dẫn giải

a) A(1;-1) thuộc vào (d) nên: -1 = (2a-1).1 -3 ⇔ 2a = 3 ⇔ a = 3/2

Phương trình đường thẳng (d): y=(2. 3/2 – 1)x – 3 ⇔ y = 2x – 3.

b) Phương trình đường thẳng (d’) có dạng y = a’x+b’

(d’) vuông góc với (d) ⇔ a’.2 = -1 ⇔ a’ = -1/2

Vậy (d’): y= -1/2x + b

Tọa độ điểm B(0; 4/3) thuộc (d) ⇔ 4/3 = -1/2.0 + b ⇔ b = 4/3

Phương trình đường thẳng (d’): y= -1/2x + 4/3

c, Phương trình hoành độ giao điểm C giữa (d) và (d’):

2x-3 = -1/2x + 4/3

2x+ 1/2x= 4/3 + 3

5/2x = 13/3

x = 26/15

=> y = 2.26/15 – 3 = 7/15

Vậy C(26/15; 7/15)