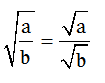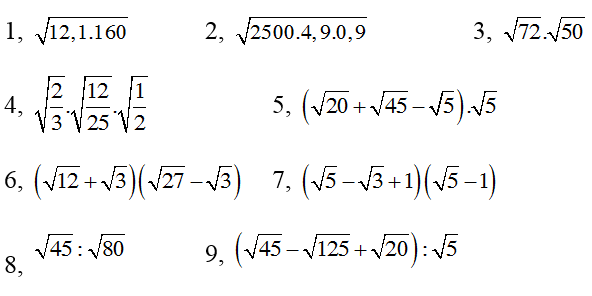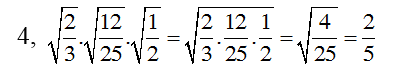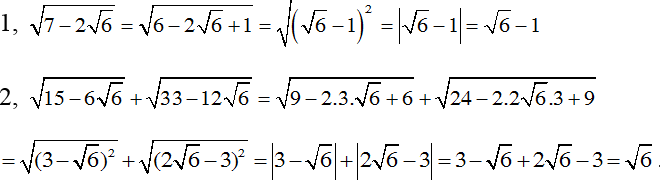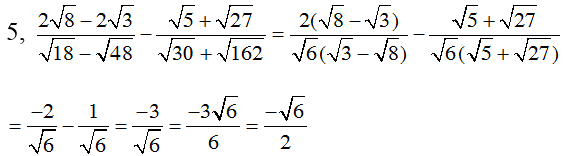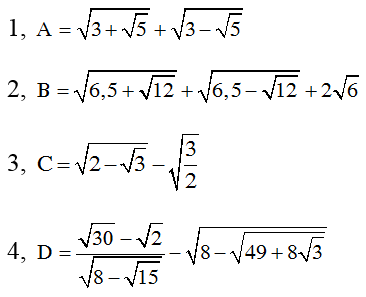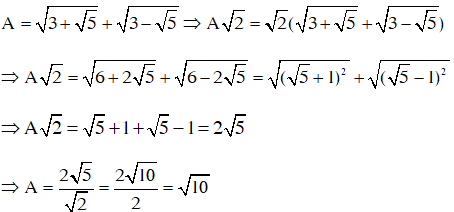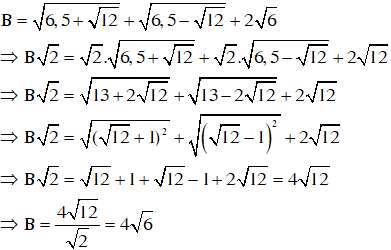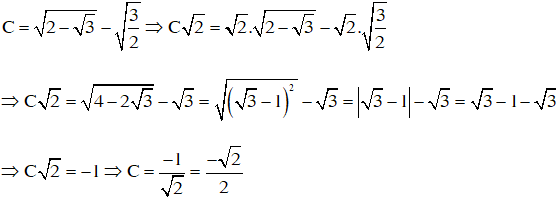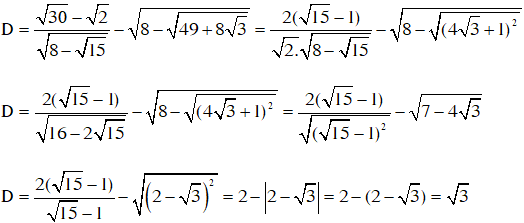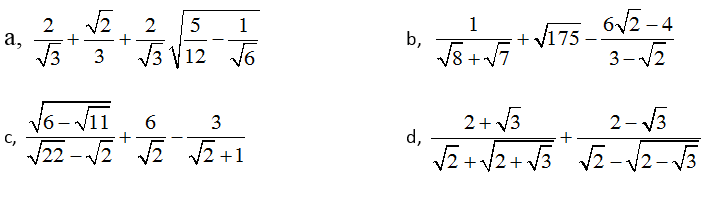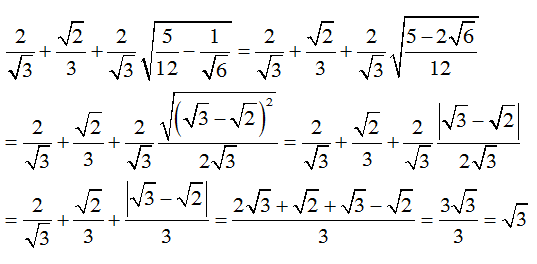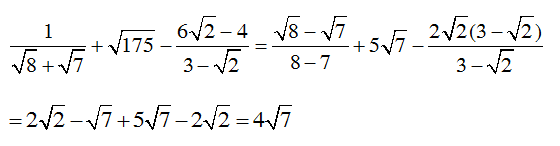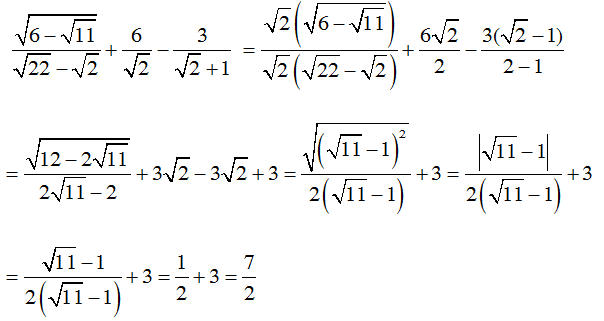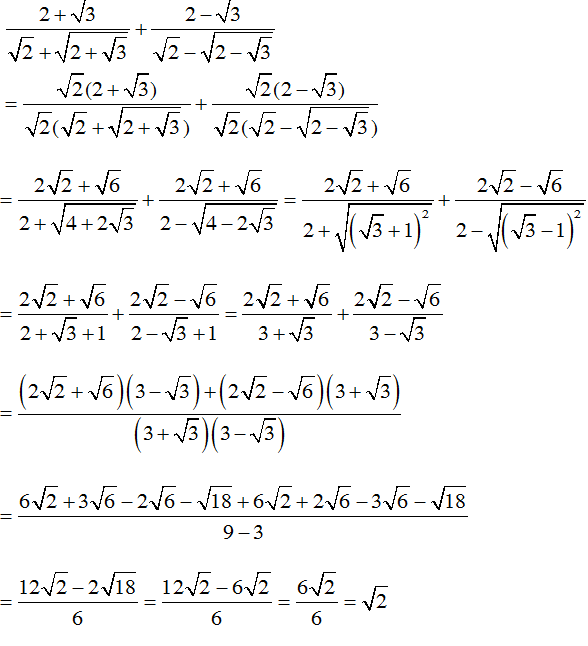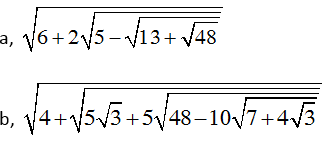Biến đổi căn thức bậc hai đơn giản
A. Phương pháp giải
Dựa vào quy tắc nhân các căn bậc hai:
– Với a,b ≥ 0 thì √a . √b = √ab .
– Với a ≥ 0, b≥ 0 thì
Sau đó thực hiện các phép biến đổi đơn giản biểu thức chứa căn rồi thu gọn các căn thức đồng dạng hoặc rút gọn.
B. Bài tập tự luận
Bài 1:
Đưa thừa số vào trong dấu căn
a, 3√5
b, 2/7√35
c, -4√(1/8)
d, -0,06√250
e, x√x
f, y√(x/y)
Hướng dẫn giải
a. 3√5 = √(32.5) = √45
b. 2/7√35 = √((2/7)2. 35)= √20/7
c. -4√(1/8) = -√(42.1/8) = -√2
d. -0,06√250 = -√(0,06)2.250 = -√0,9
e. x√x = √(x2.x) = √x3
f. y√(x/y) = √y2.(x/y)= √(xy)
Bài 2:
Thực hiện phép tính
Hướng dẫn giải
1. √(12,1. 160) = √12,1 . √160 = √121 . √16 = 11 . 4 = 44
2. √(2500.4,9.0,9) = √(25.49.9) = √25 . √49 √9 = 5 .7 . 3 = 105
3. √72 . √50 = √(72.50) = √(36.100) = √36 . √100 = 6.10 =60
5. (√20 + √45 – √5)√5 = √100 + √225 – √25 = 10 + 15 – 5 = 20
6. (√12 + √3)(√27 – √3) = √324 – √36 + √81 -√9 = 18 – 6 + 9 – 3 = 18
7. (√5 – √3 + 1)(√5 – 1) = 5 – √5 – √15 +√3 + √5 – 1 = 4 – √15 + √3
8. √45 : √80 = √(45/80) = √(9/16) = √(3/4)
9. (√45 – √125 + √20) : √5 = √9 – √25 + √4 = 3 – 5 + 2 = 0
Bài 3:
Thực hiện phép tính sau:
Hướng dẫn giải
3. 5√48 – 4√27 – 2√75 + √108 = 5√(42.3) – 4√(32.3) – 2√(52.3) + √(62.3)
= 20√3 – 12√3 – 10√3 + 6√3 = 4√3
4. 10√28 + 2√275 – 3√343 – 3/2√396
= 10√(4.7) + 2√(11.25) – 3√(73) – 3/2√(36.11)
= 20√7 + 10√11 – 21√7 -3/2.6√11
= √11 – √7
Bài 4: Thực hiện phép tính
Hướng dẫn giải
1.
2.
3.
4.
Bài 5: Rút gọn biểu thức sau
Hướng dẫn giải
a.
b.
c.
d.
Bài 6:
Rút gọn biểu thức sau
Hướng dẫn giải
a.
b.