Các bài hình lớp 9 hay thi vào 10 (phần 4). Tiếp tục là các series bài hình hay thi vào 10 do thầy Thế Anh biên soạn giúp cá em thi vào 10 hiệu quả.

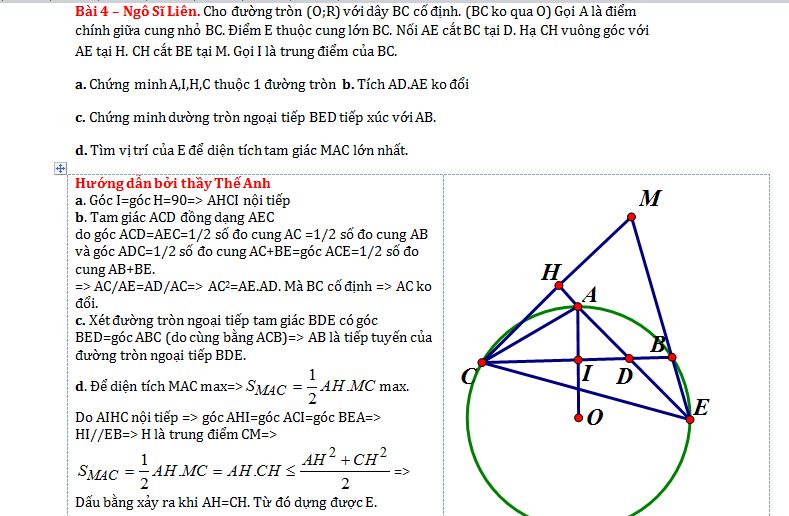
Bài 4 – Ngô Sĩ Liên. Cho đường tròn (O;R) với dây BC cố định. (BC ko qua O) Gọi A là điểm chính giữa cung nhỏ BC. Điểm E thuộc cung lớn BC. Nối AE cắt BC tại D. Hạ CH vuông góc với AE tại H. CH cắt BE tại M. Gọi I là trung điểm của BC.

a. Chứng minh A,I,H,C thuộc 1 đường tròn b. Tích AD.AE ko đổi
c. Chứng minh dường tròn ngoại tiếp BED tiếp xúc với AB.
d. Tìm vị trí của E để diện tích tam giác MAC lớn nhất.
Hướng dẫn bởi thầy Thế Anh
a. Góc I=góc H=90=> AHCI nội tiếp
b. Tam giác ACD đồng dạng AEC
do góc ACD=AEC=1/2 số đo cung AC =1/2 số đo cung AB và góc ADC=1/2 số đo cung AC+BE=góc ACE=1/2 số đo cung AB+BE.
=> AC/AE=AD/AC=> AC2=AE.AD. Mà BC cố định => AC ko đổi.
c. Xét đường tròn ngoại tiếp tam giác BDE có góc BED=góc ABC (do cùng bằng ACB)=> AB là tiếp tuyến của đường tròn ngoại tiếp BDE.
d. Để diện tích MAC max=> max.
Do AIHC nội tiếp => góc AHI=góc ACI=góc BEA=> HI//EB=> H là trung điểm CM=> => Dấu bằng xảy ra khi AH=CH. Từ đó dựng được E.

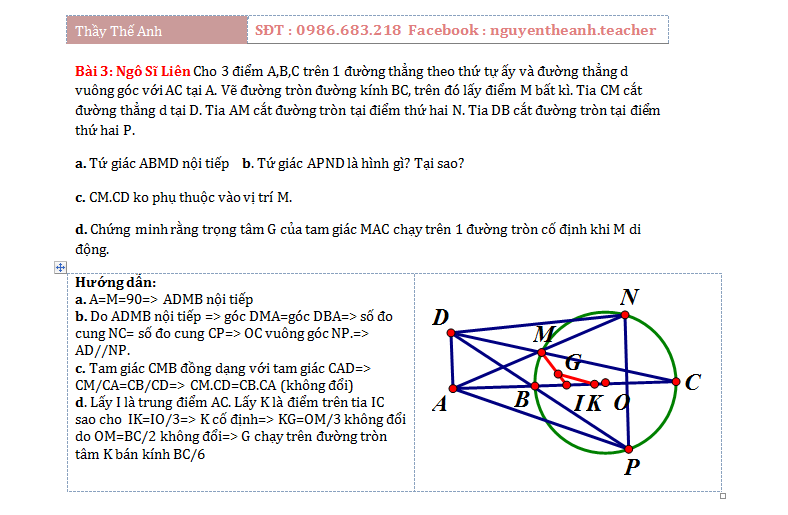
Bài 3: Ngô Sĩ Liên Cho 3 điểm A,B,C trên 1 đường thẳng theo thứ tự ấy và đường thẳng d vuông góc với AC tại A. Vẽ đường tròn đường kính BC, trên đó lấy điểm M bất kì. Tia CM cắt đường thẳng d tại D. Tia AM cắt đường tròn tại điểm thứ hai N. Tia DB cắt đường tròn tại điểm thứ hai P.

a. Tứ giác ABMD nội tiếp b. Tứ giác APND là hình gì? Tại sao?
c. CM.CD ko phụ thuộc vào vị trí M.
d. Chứng minh rằng trọng tâm G của tam giác MAC chạy trên 1 đường tròn cố định khi M di động.
Hướng dẫn:
a. A=M=90=> ADMB nội tiếp
b. Do ADMB nội tiếp => góc DMA=góc DBA=> số đo cung NC= số đo cung CP=> OC vuông góc NP.=> AD//NP.
c. Tam giác CMB đồng dạng với tam giác CAD=> CM/CA=CB/CD=> CM.CD=CB.CA (không đổi)
d. Lấy I là trung điểm AC. Lấy K là điểm trên tia IC sao cho IK=IO/3=> K cố định=> KG=OM/3 không đổi do OM=BC/2 không đổi=> G chạy trên đường tròn tâm K bán kính BC/6

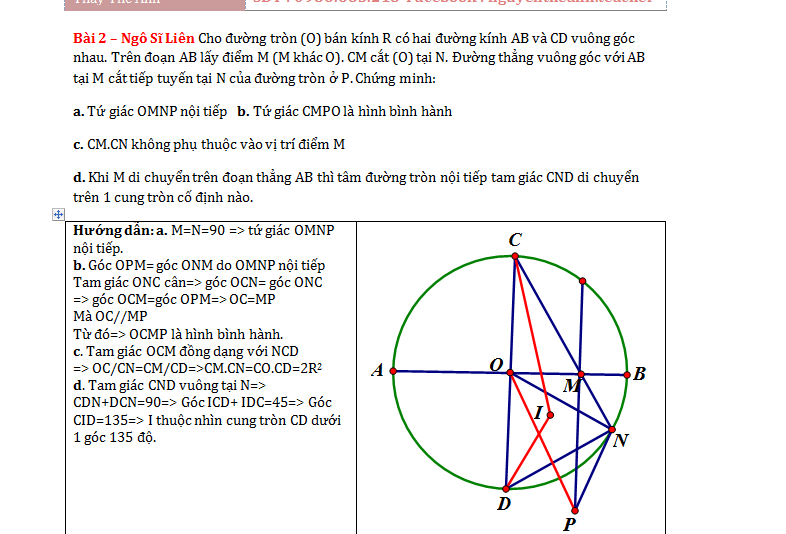
Bài 2 – Ngô Sĩ Liên Cho đường tròn (O) bán kính R có hai đường kính AB và CD vuông góc nhau. Trên đoạn AB lấy điểm M (M khác O). CM cắt (O) tại N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở P. Chứng minh:

a. Tứ giác OMNP nội tiếp b. Tứ giác CMPO là hình bình hành
c. CM.CN không phụ thuộc vào vị trí điểm M
d. Khi M di chuyển trên đoạn thẳng AB thì tâm đường tròn nội tiếp tam giác CND di chuyển trên 1 cung tròn cố định nào.
Hướng dẫn: a. M=N=90 => tứ giác OMNP nội tiếp.
b. Góc OPM= góc ONM do OMNP nội tiếp
Tam giác ONC cân=> góc OCN= góc ONC
=> góc OCM=góc OPM=> OC=MP
Mà OC//MP
Từ đó=> OCMP là hình bình hành.
c. Tam giác OCM đồng dạng với NCD
=> OC/CN=CM/CD=>CM.CN=CO.CD=2R2
d. Tam giác CND vuông tại N=> CDN+DCN=90=> Góc ICD+ IDC=45=> Góc CID=135=> I thuộc nhìn cung tròn CD dưới 1 góc 135 độ.