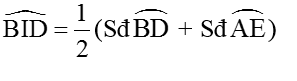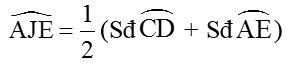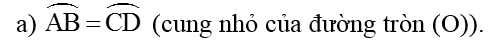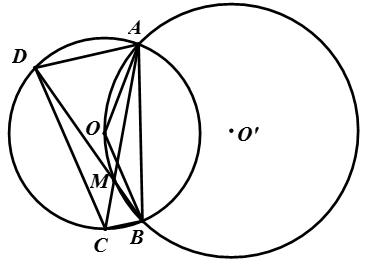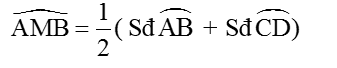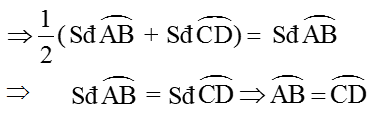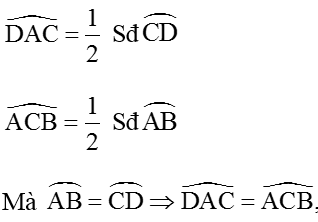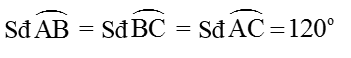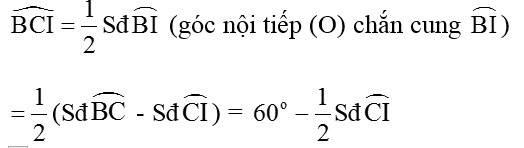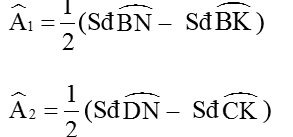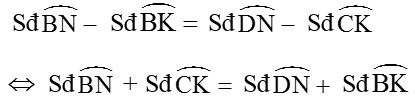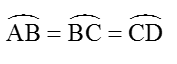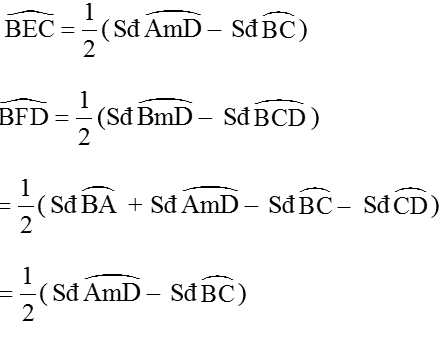Góc có đỉnh bên trong, góc có đỉnh bên ngoài đường tròn

A. Phương pháp giải

Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bi chắn (một cung nằm giữa hai cạnh của góc và cung kia nằm giữa các tia đối của hai cạnh ấy).

Số đo của góc có đỉnh nằm ngoài đường tròn bằng nửa hiệu của số đo của hai cung bị chắn.

B. Bài tập tự luận

Bài 1:

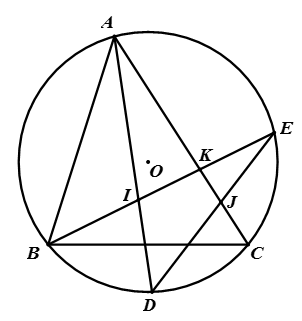
Cho ΔABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ (O)). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Chứng minh rằng:

a) ∠BID = ∠AJE .

b) AI.JK = IK.EJ.

Hướng dẫn giải

∠AJE là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung CD và AE

Mà AD là phân giác của góc A nên

Suy ra ∠BID = ∠ẠJE

b) Xét ΔAIK và ΔEJK có:

+) ∠AKI = ∠EKJ (đối đỉnh)

+) ∠IAK = ∠KEJ (hai góc nội tiếp chắn hai cung bằng nhau BD và cung CD )

Do đó ΔAIK ∼ ΔEJK (g.g)

=> AI/EJ = IK/JK => AI.JK = IK.EJ

Bài 2:

Cho hai đường tròn (O) và (O’) cắt nhau tại 2 điểm A, B sao cho O ≠ (O’). Lấy điểm M thuộc đường tròn (O’), M ở trong đường tròn (O). Tia AM và BM cắt đường tròn (O) lần lượt tại C và D. Chứng minh rằng:

b) Tứ giác ABCD là hình thang cân.

Hướng dẫn giải

a) Vì ∠AMB là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung AB và CD nên:

Mặt khác: ∠AMB = ∠AOB (hai góc nội tiếp (O’) cùng chắn cung AB lớn)

∠AOB = Sđ AB (góc ở tâm đường tròn (O)).

b) Trong đường tròn (O):

Vì hai góc này ở vị trí so le trong,

suy ra AD // BC (1)

Theo câu a), ta có: ∠ADC = ∠DAB (2 góc chắn 2 cung bằng nhau)

Từ (1) và (2) suy ra tứ giác ABCD là hình thang cân.

Bài 3:

Cho ΔABC đều nội tiếp đường tròn (O). Điểm I chuyển động trên cung nhỏ BC. AB cắt CI tại M, AC cắt BI tại N. Chứng minh rằng:

a) BC²= BM.CN

b) ∠AIN có số đo không đổi.

Hướng dẫn giải

a) Vì ΔABC đều nên:

Ta có: ∠ANB là góc có đỉnh ngoài đường tròn (O) nên:

Lại có:

Suy ra ∠ANB = ∠BCI (1)

Tương tự ta có: ∠AMC = ∠CBI (2)

Từ (1) và (2) suy ra: ΔBCM ∼ ΔCNB => BC/NC = BM/BC => BC² = BM.NC

b) Ta có: ∠AIB = ∠ACB = 60^o

=> ∠AIN = 180^o – ∠AIB = 120^o không đổi

Bài 4:

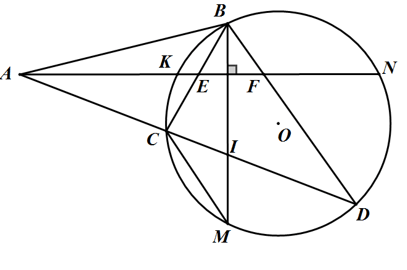
Qua điểm A nằm ngoài đường tròn (O) vẽ tiếp tuyến AB và cát tuyến ACD với đường tròn (C nằm giữa A và D). Vẽ dây BM vuông góc với tia phân giác của ∠BAC, BM cắt CD tại I. Chứng minh rằng:

a) BM là tia phân giác của

b) MD² = MI.MB

Hướng dẫn giải

Giả sử tia phân giác của ∠BAC cắt BC tại E, cắt BD tại E và cắt đường tròn (O) tại K.

a) Ta có:

Mà ∠A₁ = ∠A₂ (gt)

⇔ ∠BEF = ∠BFE

=> ΔBEF cân tại B.

Mà BM là đường cao của ΔBEF

Suy ra BM là tia phân giác của ∠CBD

b) Vì BM là phân giác của ∠CBD

Do đó: ΔMDI ∼ ΔMBD (g.g)

=> MD² = MI.MB

Bài 5:

Cho đường tròn (O) và dây cung AB, CD cắt nhau tại điểm E nằm ngoài đường tròn. Đường thẳng kẻ từ E song song với AD cắt BC tại F. Kẻ tiếp tuyến FG với đường tròn (O). Chứng minh rằng:

b) ΔFEC ∼ ΔFBE, từ đó suy ra EF² = FB.FC

Hướng dẫn giải

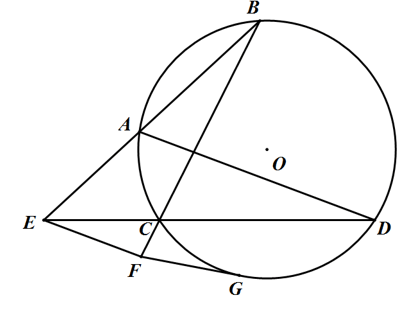
Gọi I là giao điểm AD và BC.

a) Vì AD // EF => ∠EFC = ∠AIB (đồng vị)

b) Ta có: ∠ABC = ∠ADC = 1/2 SđAC

Mà AD // EF => ∠ADC = ∠DEF (so le trong)

Do đó: ΔFEC ∼ ΔFBE

Do đó EF² = FB.FC

Bài 6:

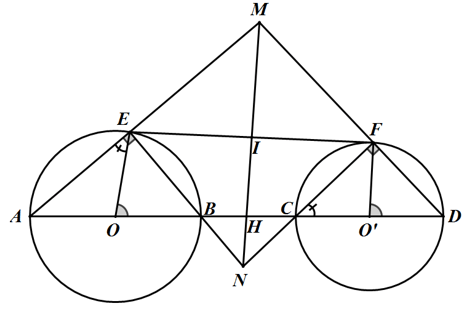
Cho hai đường tròn (O) và (O’) ở ngoài nhau. Đường thẳng OO’ cắt (O) và (O’) lần lượt lại các điểm A, B, C, D. Kẻ tiếp tuyến chung ngoài EF của hai đường tròn (E ≠ (O), F ≠ (O’)) . Gọi M là giao điểm của AE và DF, N là giao điểm của EB và DC. Chứng minh rằng:

a) Tứ giác MENF là hình chữ nhật.

b) MN ⊥ AD

c) ME.MA = MF.MD.

Hướng dẫn giải

a) Ta có: ∠AEB = ∠CFD = 90^o

Vì EF là tiếp tuyến chung của hai đường tròn (O) và (O’) nên

OE ⊥ EF

OF’ ⊥ EF

=> OE // OF’

=> ∠EOB = ∠FO’D (đồng vị)

=> ∠EAO = ∠FCO’

Do đó MA // FN, mà EB ⊥ MA => EB ⊥ FN.

Hay ∠FNB = 90^o

Tứ giác MENF có ∠E = ∠N = ∠F = 90^o nên là hình chữ nhật.

b) Gọi I là giao điểm của MN và EF, H là giao điểm của MN và AD. Vì tứ giác MENF là hình chữ nhật nên ∠IFN = ∠INF .

Mặt khác trong đường tròn (O’): ∠FDO = ∠IFN = 1/2Sđ FC.

Do đó: ∠FDC = ∠HNC

Suy ra: ΔFDC ∼ ΔHNC (g.g) => ∠NHC = ∠DFC = 90^o hay MN ⊥ AD

c) Ta có: ∠MFE = ∠FEN (do MENF là hình chữ nhật).

Trong đường tròn (O): ∠FEN = ∠EAB = 1/2Sđ EB

Do đó:∠MFE = ∠EAB .

Suy ra: ΔMEF ∼ ΔMDA (g.g)

=> ME/MD = MF/MA => ME.MA = MF.MD

Bài 7:

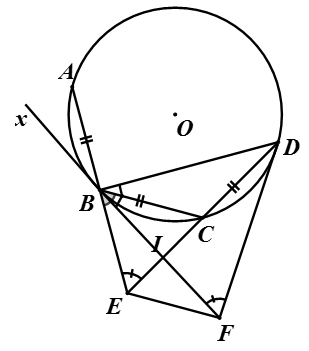
Trên đường tròn (O; R) đặt liên tiếp các dây cung: AB = BC = CD < R. AB cắt CD tại E. Tiếp tuyến tại B và D với đường tròn (O) cắt nhau tại F. Chứng minh rằng:

a) ΔEBC ∼ ΔFBD

b) ΔEBF ∼ ΔCBD

c) BC // EF.

Hướng dẫn giải

Do AB = BC = CD nên

a) Ta có:

Vậy: ∠BEC = ∠BFD (1)

Ta có: ∠DBC = ∠CBF = 1/2Sđ BC = 1/2Sđ AB = ∠ABx = ∠FBE

Suy ra: ∠CBE = ∠DBF (2)

Từ (1) và (2) suy ra: ΔBCE ∼BDF (g.g)

b) Ta có: ∠EBF = ∠CBD .

Mặt khác theo câu a) suy ra: BF/BE = BD/BC

Do đó: ΔBCE ∼ ΔCBD (g.g)

c) Vì ∠EFB = ∠CDB = ∠CBF

Mà ∠EFB và ∠CBF ở vị trí so le trong nên BC // EF.

Bài 8:

Cho tứ giác ABCD có A, B, C, D nằm trên đường tròn (O); AB và CD cắt nhau tại M; AD và BC cắt nhau tại N.

a) Tính số đo các góc của tứ giác ABCD nếu ∠AMD = 30^o và ∠BND = 40^o .

b) Hai phân giác của góc M và góc N cắt nhau tại I. Chứng minh rằng IM ⊥ IN

Hướng dẫn giải

a) Trong đường tròn (O):

ΔCND có : ∠N + ∠D + ∠C = 180^o (1)

ΔAMD có : ∠A + ∠D + ∠M = 180^o (2)

=> ∠M + ∠N + ∠A + ∠C + 2∠D = 360^o

=> ∠D = 55^o

Thay vào (1) suy ra ∠C = 85^o

Thay vào (2) suy ra ∠A = 95^o

Do đó ∠B = 125^o .

b) Giả sử MI cắt đường tròn (O) tại hai điểm E và F; cắt NC, ND lần lượt tại P và Q.

Vì MI là phân giác của góc ∠M nên ∠AMF = ∠DMF

=> ΔNPQ cân tại N

Mặt khác: NI là phân giác của ∠N, suy ra NI ⊥ PQ hay MI ⊥ NI