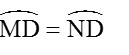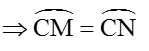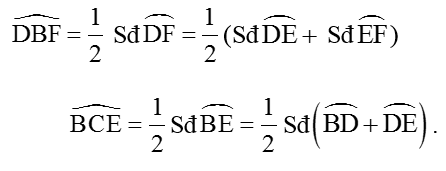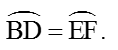Góc nội tiếp

A. Phương pháp giải

1. Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

2. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.

3. Trong một đường tròn:

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

c) Góc nội tiếp (nhỏ hơn hoặc bằng) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

d) Góc nội tiếp chắn nửa đường tròn là góc vuông.

Bài 1:

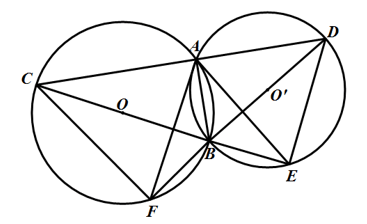
Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B . Vẽ cát tuyến CAD vuông góc với AB . Tia CB cắt (O’) tại E, tia BD cắt (O) tại F. Chứng minh rằng:

a) ∠CAF = ∠DAE

b) AB là tia phân giác của

c) CA.CD = CB.CE

d) CD² = CB.CE + BD.CF

Hướng dẫn giải

Vì CD ⊥ AB => ∠CAB = 90^o

Mà ∠CAB = 1/2 Sđ BC => Sđ BC = 180^o

Vậy ba điểm B, O, C thằng hàng.

Chứng minh tương tự ta có B, O’, D thẳng hàng.

a) Trong (O) ta có: ∠CAF = ∠CBF (góc nội tiếp cùng chắn cung CF )

Trong (O’) ta có: ∠DAE = ∠DBE (góc nội tiếp cùng chắn cung DE )

Mà ∠CBF = ∠DBE (đối đỉnh)

Suy ra: ∠CAF = ∠DAE .

b) Nối CF và DE ta có: ∠CFB = 90^o (góc nội tiếp chắn nữa đường tròn (O))

∠BED = 90 ^o (góc nội tiếp chắn nửa đường tròn (O’))

Xét ΔCFB và ΔDEB có:

∠CDB = ∠BED = 90^o

∠CBF = ∠DBE (đối đỉnh)

=> ∠FCB = ∠EDB

Mặt khác: ∠FAB = ∠FCB (góc nội tiếp (O) cùng chắn cung FB )

∠EAB = ∠EDB (góc nội tiếp (O’) cùng chắn cung EB )

Suy ra: ∠FAB = ∠EAB hay AB là phân giác của góc ∠EAF .

c) Xét ΔCAE và ΔCBD có: ∠C chung

∠CEA = ∠BDA (góc nội tiếp (O’) cùng chắn cung AB)

=> ΔCAE ∼ ΔCBD (g.g)

=> CA/CB = CE/CD hay CA.CD = CB.CE (1)

d) Chứng minh tương tự câu c) ta có: DA.DC = DB.DF (2)

Từ (1) và (2) suy ra:

CA.CD + DA.DC = CB.CE + DB.DF

⇔ (CA + DA)CD = CB.CE + DB.DF

⇔ CD² = CB.CE + DB.DF

Bài 2:

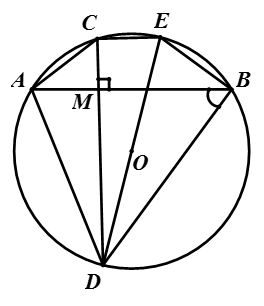
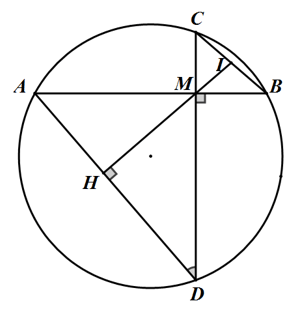
Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh rằng:

a) MA.MB = MC.MD.

b) Tứ giác ABEC là hình thang cân.

c) Tổng có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Hướng dẫn giải

a) Xét ΔAMC và ΔDMB có:

∠ACD = ∠ABD (góc nội tiếp cùng chắn cung AD)

∠AMC = ∠BMD = 90^o (gt)

=> ΔAMC ∼ ΔDMB (g.g)

=> MA/MD = MC/MB => MA.MB = MC.MD

b) Vì ∠DCE = 90^o (góc nội tiếp chắn nửa đường tròn)

=> CD ⊥ CE

CD ⊥ AB (gt)

=> AB // CE.

=> Tứ giác ABEC là hình thang (1).

Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE nên

Từ (1) và (2) suy ra tứ giác ABEC là hình thang cân.

c)

=> EB = BC .

Mặt khác: ∠DAE = 90^o (góc nội tiếp chắn nửa đường tròn)

Do đó: MA² + MB² + MC² + MD²

= (MA²+ MD²) + (MB² + MC²)

= AD² + BC² = DE² = 4R² không đổi

Bài 3:

Cho ΔABC nội tiếp đường tròn (O; R), kẻ AH ⊥ BC, AO cắt (O) tại D. Chứng minh rằng:

a) ΔABH ∼ ΔADC .

b) S= abc/4R (S: diện tích tam giác ABC; a, b, c: độ dài cạnh của ΔABC)

Hướng dẫn giải

a) Xét ΔABH và ΔADC có:

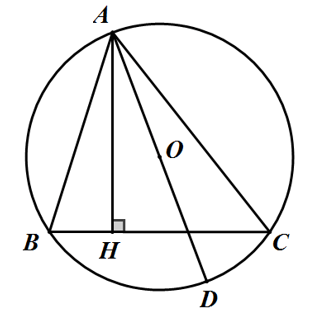
Xét ΔABH và ΔADC có:

∠AHB = ∠ACD = (90^o)

∠ABC = ∠ADC (góc nội tiếp cùng chắn cung AC )

=> ΔABH ∼ ΔADC

b) Vì ΔABH ∼ ΔADC => AB/AD = AH/AC

=> AH = AB.AC/AD = bc/2R

Do đó diện tích tam giác ABC là:

S= 1/2 AH.BC = 1/2 . bc/2R. a = abc/4R

Bài 4:

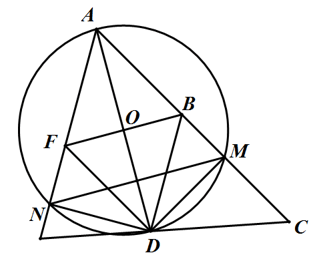
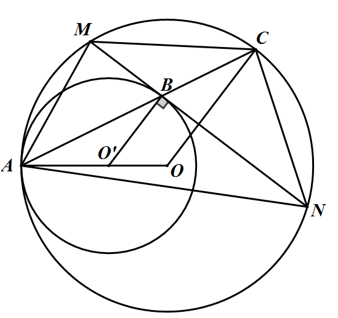
Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM.

a) Chứng minh ΔACN = ΔBCM .

b) Chứng minh ΔCMN vuông cân.

c) Tứ giác ANCD là hình gì? Vì sao?

Hướng dẫn giải

a) Xét ΔACN và ΔBCM có:

+ AC = BC (vì C là điểm chính giữa cung AB)

+ ∠CAN = ∠CBN (hai góc nội tiếp cùng chắn cung CM)

+ AN = BM (gt)

=> ΔACN = ΔBCM (c.g.c)

b) Vì ΔACN = ΔBCM (chứng minh a)

=> CN = CM => ΔCMN cân tại C (1)

Lại có ∠CMA = 1/2Sđ AC = 1/2. 90^o = 45^o

Từ (1) và (2) suy ra ΔCMN vuông cân tại C.

Vì CD // AM nên tứ giác ADCM là hình thang cân.

Ta có: ∠DAM = ∠CMN = ∠CNM = 45^o

Suy ra: AD // CN.

Vậy tứ giác ADCN là hình bình hành.

Bài 5:

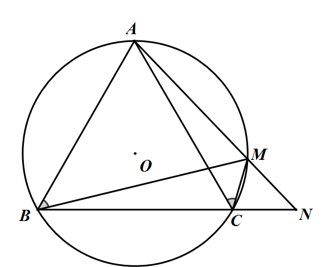
Cho ΔABC cân tại A nội tiếp đường tròn (O). M là một điểm bất kỳ thuộc cung nhỏ AC. Tia AM cắt BC tại N. Chứng minh rằng:

a) AB₂ = AM.AN

b) ∠ACM = ∠ANC

Hướng dẫn giải

a) Vì ΔABC cân tại A nên ∠ABC = ∠ACB

Lại có ∠ACB = ∠AMB (góc nội tiếp cùng chắn cung AB )

Suy ra: ∠ABN = ∠AMB

Do đó: ΔABM ∼ ΔANB (g.g)

=> AB/AN = AM/MB

=> AB² = AN. AM

b) Vì ΔABM ∼ ΔANB => ∠ABM = ∠ANB

Mà ∠ABM = ∠ACM (góc nội tiếp cùng chắn cung AM)

Do đó: ∠ACM = ∠ANC

Bài 6:

Cho ΔABC có AD là tia phân giác trong của góc A. Qua D kẻ đường thẳng song song với AB cắt AC ở E và đường thẳng song song với AC cắt AB ở F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Đường tròn đường kính AD cắt AB và AC lần lượt tại các điểm M và N. Chứng minh: MN // EF.

Hướng dẫn giải

ΔABC có AD là tia phân giác trong của góc A

=> ∠BAD = ∠CAD

=>

=> ∠DAC = ∠MND (góc nội tiếp chắn hai cung bằng nhau)

Lại có: ∠AND = 90^o (nội tiếp chắn nửa đường tròn)

=> ∠DAN + ∠ADN = 90^o

=> ∠MND + ∠ADN = 90^o

=> MN // AD

Vì tứ giác AEDF là hình thoi nên EF ⊥ AD => MN // EF

Bài 7:

Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc trong với nhau tại A, (R > R’). Qua điểm B bất kỳ trên (O’) vẽ tiếp tuyến với (O’) cắt (O) tại hai điểm M và N, AB cắt (O) tại C. Chứng minh rằng:

a) MN ⊥ OC

b) AC là tia phân giác của ∠MAN

Hướng dẫn giải

a) Vì Δ O’AB cân tại O’ nên ∠O’AB = ∠O’BA

Δ OAC cân tại O nên ∠OAC = ∠OCA

Suy ra ∠O’BA = ∠OCA, mà hai góc này ở vị trí đồng vị, do đó O’B // OC.

Mặt khác MN là tiếp tuyến của (O’) tại B

=> O’B ⊥ MN. Do đó OC ⊥ MN

b) Trong đường tròn (O):

=> OC là đường trung trực của MN

=> CM = CN

=> ∠MAC = ∠NAC

Hay AC là tia phân giác của ∠MAN .

Bài 8:

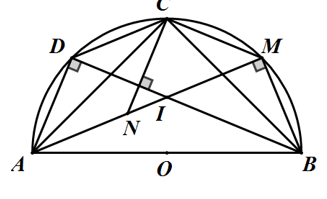
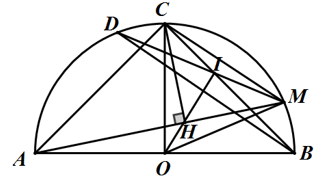
Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa cung AB. M là điểm bất kỳ trên cung BC, kẻ CH ⊥ AM.

a) Chứng minh ΔHCM vuông cân và OH là tia phân giác của ∠COM

b) Gọi I là giao điểm của OH với BC và D là giao điểm của MI với nửa đường tròn (O). Chứng minh MC // BD.

Hướng dẫn giải

ΔHCM vuông cân tại H.

Do đó CH = HM

Dễ thấy ΔCOH = ΔMOH (c.c.c)

=> ∠COH = ∠MOH

Vậy OH là tia phân giác của ∠COM

b) Dễ thấy ΔCOI = ΔMOI (c.g.c) nên CI = MI => ΔCMI cân tại M.

Do đó ∠CMI = ∠MCI.

Lại có ∠CMD = ∠CBD (góc nội tiếp cùng chắn cung CD)

Suy ra ∠MCB = ∠CBD, mà hai góc này ở vị trí so le trong nên MC // BD.

Bài 9:

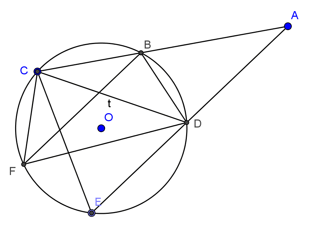
Qua điểm A nằm ngoài đường tròn (O) kẻ hai cát tuyến ABC và ADE với đường tròn đó (B nằm giữa A và C, A nằm giữa A và E). Kẻ dây BF // DE. Chứng minh rằng:

a) ∠DBF = ∠BCE

b) ΔACE ∼ ΔDCF

Hướng dẫn giải

a) Ta có

Mặt khác DE // BF

=>

Từ đó suy ra ∠DBF = ∠BCE.

c) Vì BF // DE nên ∠CBF = ∠CAE (đồng vị)

Mà ∠CBF = ∠CDF (góc nội tiếp cùng chắn cung CF) => ∠CDF = ∠CAE (1)

Lại có ∠CED = ∠CFD (gócc nội tiếp cùng chắn cung CD) (2)

Từ (1) và (2) suy ra ΔACE ∼ ΔDCF (g.g)

Bài 10:

Qua điểm M nằm trong đường tròn (O) kẻ hai dây AB và CD vuông góc với nhau. Chứng minh rằng:

a) Đường cao MH của tam giác AMD đi qua trung điểm I của BC.

b) Đường trung tuyến MI của ΔBMC vuông góc với AD.

Hướng dẫn giải

a) Ta có ∠ADC = ∠ABC (góc nội tiếp cùng chắn cung AC) (1)

Lại có ∠AMH = ∠ADM (cùng phụ với góc ∠MAD)

Mà ∠AMH = ∠IMB (đối đỉnh)

=> ∠ADM = ∠IMB (2)

Do đó IM = IB.

Chứng minh tương tự ta có: IM = IC

Suy ra IB = IC = IM hay I là trung điểm của BC.

b) Học sinh tự chứng minh.

Bài 11:

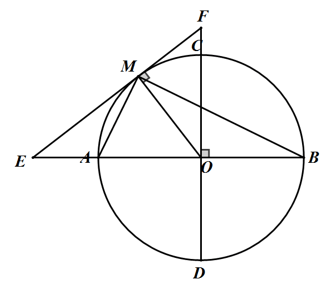
Cho AB và CD là hai đường kính vuông góc với nhau của đường tròn (O; R). Qua điểm M thuộc cung nhỏ AC (M ≠ A, M ≠ E)kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E, F.

a) Chứng minh: ∠MFO = 2.∠MBO

b) Xác định vị trí điểm M trên cung nhỏ AC sao cho ∠FEO = 30^o. Khi đó tính độ dài đoạn thẳng OE, ME, EF theo R.

Hướng dẫn giải

a) Ta có: ∠MOA = 2∠MBO (cùng chắn cung MA)

Vì EF là tiếp tuyến với (O) tại M nên OM ⊥ EF

Ta có ∠MOA = ∠EFO (cùng phụ với góc ∠FEO )

Suy ra ∠EFO = 2∠MBO

b) Ta có: ∠FEO = 30^o ⇔ ∠MOA = 60^o

⇔ ΔAOM đều nên AM = OA = R.

Vậy nếu M ∈ (O) và AM = R thì ∠FEO = 30^o

Khi đó ΔOME vuông tại M nên

ME = MO. tan∠MOA = √3R

OE = 2MO = 2R

Vì ΔEOF vuông tại O nên cos ∠FEO = EO/EF

=> EF = EO/cos ∠FEO = 2R / cos30^o = 4R√3 /3