Vị trí tương đối của 2 đường tròn
A. Phương pháp giải
1. Định lý
Hai đường tròn(O) và (O’) cắt nhau thì R-r < OO’ < R+r
Nếu hai đường tròn (O) và (O’) tiếp xúc trong thì OO’=R-r.
a, Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây cung chung.
b, Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm nắm trên đường nối tâm.
B. Bài tập tự luận
Bài 1:
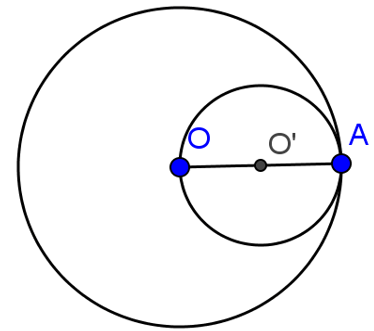
Cho đường tròn tâm O, bán kính R. Lấy điểm A tùy ý trên (O). Vẽ đường tròn đường kính OA. Xác định vị trí tương đối của hai đường tròn.
Hướng dẫn giải
Gọi O’ là tâm đường tròn đường kính OA. Ta có O’ là trung điểm của OA và bán kính đường tròn(O’) là
R’ = OA/2 = R/2.
Độ dài đoạn nối tâm: d= OO’ = OA/2 = R/2.
Ta có: R – R’ = R/2 = d nên (O) và (O’) tiếp xúc trong tại A.
Bài 2:
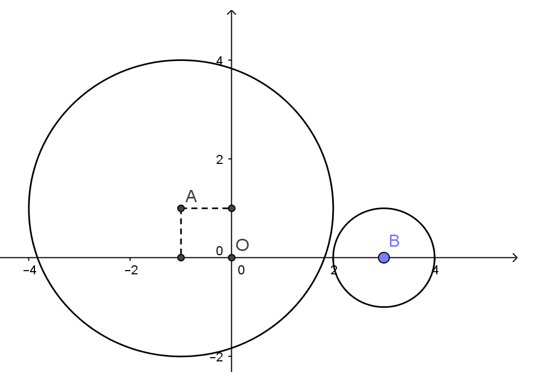
Trong mặt phẳng tọa độ xOy cho hai điểm A(-1;1) và B(3;0). Vẽ các đường tròn (A;r) và (B;r’).
Khi r=3 và r’=1, hãy xác định vị trí tương đối của hai đường tròn.
Hướng dẫn giải
Độ dài đoạn nối tâm d = AB = √(3+1)2 + 1 = √17 (1)
Tổng hai bán kính:
r + r’ = 3 + 1 = 4 (2)
Từ (1) và (2) ta thấy √17 > 4 nên hai đường tròn không giao nhau; hai đường tròn (A) và (B) nằm ngoài nhau.
Bài 3:
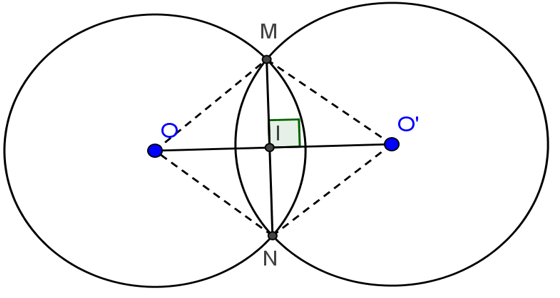
Cho hai đường tròn (O;R) và (O’; R) cắt nhau tại M và N. Biết OO’=24cm, MN=10cm. Tính R.
Hướng dẫn giải
Gọi giao điểm của OO’ và MN là I. Vì OM = ON =O’M =O’N = R nên tứ giác OMO’N là hình thoi
=> OO’ ⊥ MN tại điểm I là trung điểm của mỗi đoạn OO’ và MN.
Do đó: IM = MN/2 = 5cm ; IO = OO’/2 = 12cm.
Áp dụng định lý Py-ta-go vào tam giác MIO ta có:
R = OM = √(IM2 + IO2) = 13
Vậy R = 13(cm)
Bài 4:
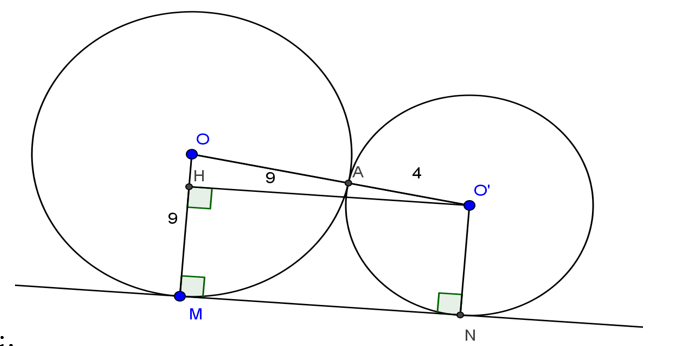
Cho hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O), N thuộc (O’). Biết R=9cm, R’= 4cm. Tính độ dài đoạn MN.
Hướng dẫn giải
Ta có: OO’= OA + O’A = 9 + 4 =13(cm)
Kẻ OH ⊥ OM tại H
Suy ra tứ giác O’NMH là hình chữ nhật
Suy ra MH=O’N=4cm; MN=O’H
Suy ra OH=OM-MH=9-4=5(cm)
Áp dụng đình lí py-ta-go vào tam giác OO’H, ta có:
MN = O’H = √(OO’2 – OH2) = 12 (cm)
Vậy MN = 12cm.