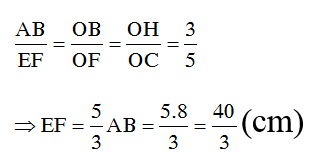Vị trí tương đối của đường thẳng với đường tròn. Tiếp tuyến của đường tròn
A. Phương pháp giải
Vị trí tương đối của đường thẳng với đường tròn.
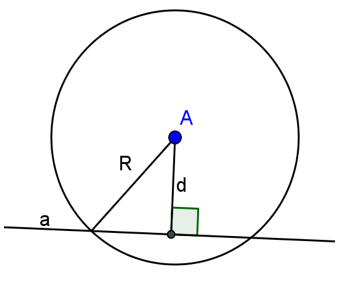
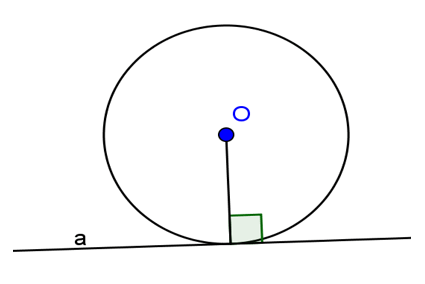

Gọi d là khoảng cách từ tâm O của đường tròn (O; R) đến đường thẳng a.
+ d < R: a cắt tại (O; R) tại 2 điểm
+ d = R: a cắt (O; R) tại 1 điểm. Trường hợp này a tiếp xúc với đường tròn hay a là tiếp tuyến của đường tròn.
+ d > R: a không căt đường tròn.
a, Định nghĩa:
Một đuờng thẳng được gọi là tiếp tuyến với đường tròn nếu nó chỉ có một điểm chung với đường tròn.
b, Định lý:
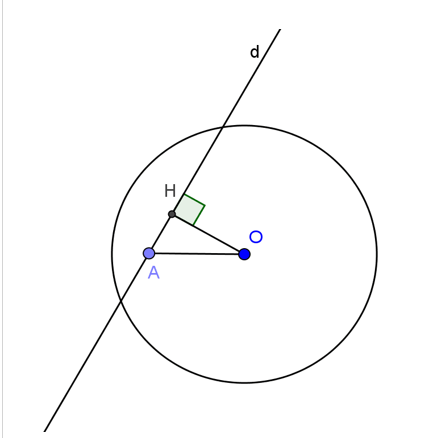
– Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
– Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn đó.
Chú ý: Để chứng minh một đường thẳng là tiếp tuyến của một đường tròn tại một điểm thuộc đương tròn, ta chứng minh đường thẳng vuông góc với bán kính qua điểm ấy của đường tròn.
B. Bài tập tự luận
Bài 1:
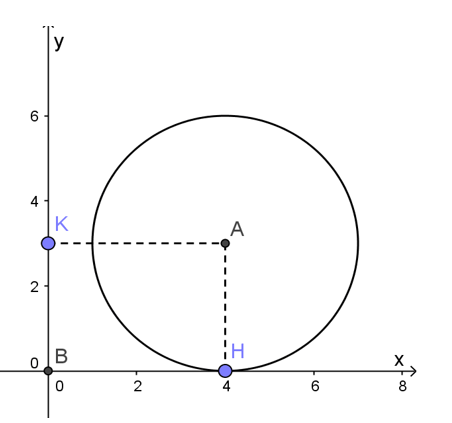
Trong hệ tọa độ Oxy cho điểm A(4;3). Hãy xác định vị trí tương đối của đường tròn tâm A, bán kính R=3 với các trục tọa độ.
Hướng dẫn giải
Khoảng cách từ A đến trục Ox là: d = AH = OK = 3.
Khoảng cách từ A đến trục Oy là d’ = AK = OH = 4.
Do đó đường tròn (A;3) tiếp xúc với trục Ox, vì d = R = 3; đường tròn (A;3) không cắt trục Oy vì d’= 4 > 3 = R.
Bài 2:
Cho điểm A nằm trong đường tròn (O). Chứng minh rằng mọi đường thẳng d đi qua A đều cắt (O) ở hai điểm phân biệt.
Hướng dẫn giải
Vì A nằm trong (O) nên OA < R.
Suy ra OH < R đường thẳng d luôn cắt (O) tại 2 điểm phân biệt.
Bài 3:
Từ điểm A cách O một khoảng d (d > R) vẽ tiếp tuyến AB với đường tròn (O;R) (B: là tiếp điểm). Tính độ dài đoạn AB.
Hướng dẫn giải
Vì AB là tiếp tuyến của (O) tại B nên AB ⊥ OB tại B Áp dụng định lý Py-ta-go vào ΔAOB có:
Bài 4:
Cho đường tròn (O;5 cm) và dây AB=8cm. Một tiếp tuyến của (O) song song với AB cắt tia OA tại E, cắt tia OB tại F. Tính độ dài EF.
Hướng dẫn giải
Gọi C là tiếp điểm của tiếp tuyến EF với (O), H là giao điểm của OC với AB.
Ta có: OC ⊥ EF tại C mà AB//EF nên OC ⊥ AB tại H.
=> HA = HB = 1/2AB = 4(cm)
Áp dụng định lý Pi-ta-go vào tam giác OHA có:
Ta có: AB//EF nên theo định lý Ta –lét ta có:
Vậy EF=40/3(cm)