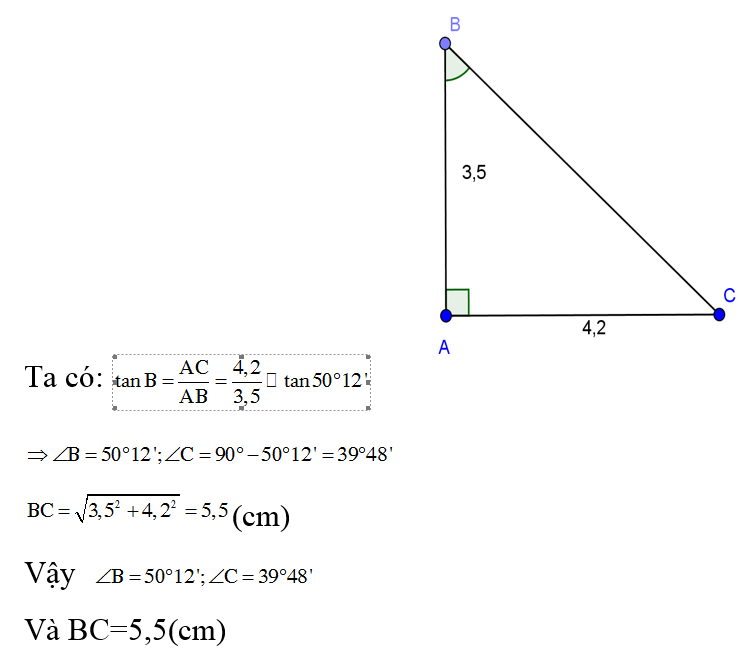Tỉ số lượng giác của góc nhọn

A. Phương pháp giải

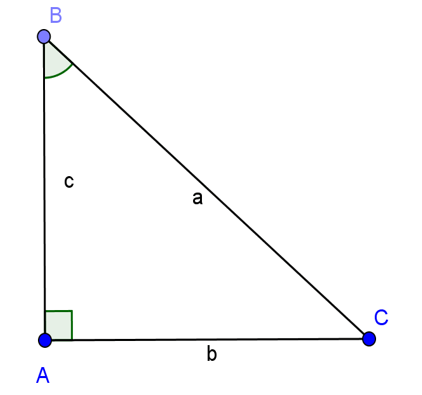
1. Định nghĩa các tỉ số lượng giác của góc nhọn:

1, sin α = AB/AC

3, tan α = AB/BC

4, cotg α = BC/AB

2. Một số tính chất của các tỉ số lượng giác

+ Cho hai góc α và β phụ nhau. Khi đó:

sin α = cos β

cos α = sin β

tan α = cotg β

cotg α = tan β

0 < sin α < 1

0 < cos α < 1

tan α = sin α / cos α

cotg α = cos α / sin α

tan α . cotg α = 1

3. Các hệ thức về cạnh và góc trong tam giác vuông.

Cho tam giác ABC vuông tại A. Khi đó:

b= a. sin B

c= a. sin C

b= a. cos C

c= a. cos B

b= c. tan B

c= b. tan C

b= c. cotg C

c= b. cotg B

B. Bài tập tự luận

Bài 1: 

Cho tam giác ABC vuông tại A, BC = a, đường cao AH.

a, Chứng minh rằng: AH=a sinBcosB; BH = a cos²B ; CH = a sin² B

b, Suy ra AB² = BC.BH ; AH² = BH.HC

Hướng dẫn giải

Xét tam giác vuông ABH, ta có:

AH = sinB.AB (1)

Xét tam giác vuông ABC, ta có:

AB = BC.cos B = acos B (2)

Từ (1) và (2) ta có:

AH = a sin B cos B

Tương tự ta có:

+ Xét tam giác vuông ABH: BH = AB.cos B

Xét tam giác vuông ABC: AB = BC.cos B = acos B => BH = a cos²B

+ Xét tam giác vuông ACH: CH = AC.cos C = AC.sin B

Tam giác vuông ABC: AC=BC.sin B=a.sin B => CH = a sin² B

b, AB² = a² cos²B

BC.BH = a.a.cos²B = a²cos²B

=> AB² = BC.BH

AH² = a²sin²cos²B

=> AH² = BH.HC

Bài 2:

Giải tam giác trong các trường hợp sau( Làm tròn đến chữ số thập phân thứ nhất).(Tức là tìm tất cả các yếu tố chưa biết của tam giác ABC)

a, Tam giác ABC vuông tại A, biết AB = 3,5; AC = 4,2.

b, Tam giác ABC vuông tại A, biết ∠B = 50^o ; AB = 3,7.

Hướng dẫn giải

Bài 3:

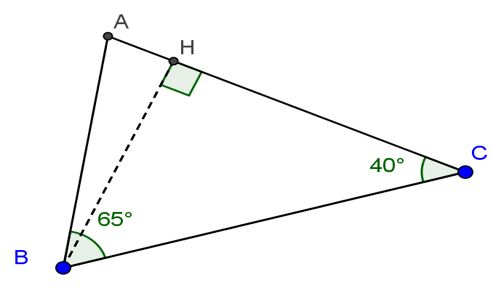
 Giải tam giác ABC, biết ∠B = 65^o; ∠C = 40^o và BC = 4,2 cm.

Hướng dẫn giải

Ta có: ∠A = 180^o – (65^o + 45^o) = 75^o

Vẽ BH ⊥ AC

+ Xét tam giác vuông HBC vuông tại H, theo hệ thức về cạnh và góc trong tam giác vuông, ta có:

BH = BC.sin C = 2,7 (cm)

Và CH = BH.cotg C (1)

+ Xét tam giác vuông ABH tại H, theo hệ thức về cạnh và góc trong tam giác vuông ta có:

BH = AB.sin A => AB = BH/sinA = 2,8 (cm) và AH = BH.cotg A (2)

Từ (1) và (2) ta có:

AC = AH+CH = BH.cotgA + BH.cotgC = BH(Cotg A+Cotg C)= 3,9(cm)

Vậy ∠A = 75^o; AB = 2,8(cm); AC = 3,9(cm).