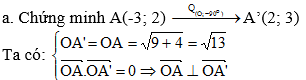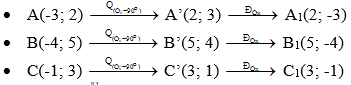Lý thuyết về phép dời hình và hai hình bằng nhau

1. Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì. Nghĩa là với hai điểm $M,N$ tùy ý và ảnh $M^{\prime },N^{\prime }$ tương ứng của chúng, ta luôn có $M^{\prime }{N}^{\prime }=MN$

2. Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng trục, đối xứng tâm và phép quay là những phép dời hình.

3. Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình là một phép dời hình.

4. Phép dời hình có các tính chất:

 a, Biến ba điểm thằng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy

 b, Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn bằng nó

 c, Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó

 d, Biến đường tròn thành đường tròn có cùng bán kính

5. Nếu một phép dời hình biến tam giác $ABC$ thành tam giác $A^{\prime }{B}^{\prime }{C}^{\prime }$ thì nó cũng biến trọng tâm, trực tâm, tâm các đường trọn nội tiếp, ngoại tiếp.. của tam giác $ABC$ tương ứng thành trọng tâm, trực tâm, tâm các đường trọng nội tiếp, ngoại tiếp… của tam giác $A^{\prime }{B}^{\prime }{C}^{\prime }$.

6. Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

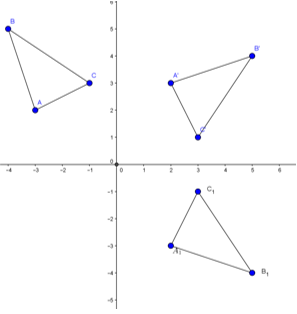
Bài 1 (trang 23 SGK Hình học 11): Trong mặt phẳng Oxy cho các điểm A(-3; 2), B(-4; 5) và C(-1; 3).

a. Chứng minh rằng các điểm A’(2; 3), B’(5; 4) và C’(3; 1) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc –90^o.

b. Gọi tam giác A₁B₁C₁ là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc –90^o và phép đối xứng qua trục Ox. Tìm tọa độ các đỉnh của tam giác A₁B₁C₁.

Lời giải:

*Hình vẽ cho thấy góc lượng giác (OA, OA’) = – 90 .

• Tương tự, phép quay Q_(O,-90^o) biến B(-4; 5) thành B’(5; 4)

• Tương tự, phép quay Q_(O,-90^o) biến C(-1; 3) thành C’(3; 1).

b. Tọa độ của A₁, B₁, C₁

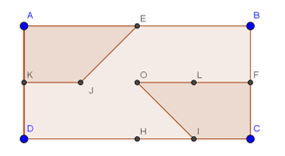
Bài 2 (trang 24 SGK Hình học 11): Cho hình chữ nhật ABCD. Gọi E, E, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, DA, KF, HC, KO. Chứng minh hai hình thang AEJK và FOIC bằng nhau.

Lời giải:

Gọi L là trung điểm của OF. Từ các dữ kiện của giả thiết, nếu thực hiện phép đối xứng trục EH thì A →B ; K → F; J → L và hình thang AEJK → hình thang BELF.

Thực hiện tiếp theo phép tịnh tiến theo vectơ EO , ta có B → F ; E → O; L → I; F → G và hình thang BELF → hình thang FOIC.

Vậy nếu thực hiện liên tiếp phép đối xứng trục EH và phép tịnh tiến theo vectơ EO thì hình thang AEJK biến thành hình thang hình thang FOIC. Vậy hai hình thang này bằng nhau.

Chú ý: Có thể thực hiện phép tịnh tiến theo vectơ EO trước và tiếp theo là phép đối xứng trục EH, ta cũng có kết quả trên.

 Bài 3 (trang 24 SGK Hình học 11): Chứng minh rằng: Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm của tam giác ABC tương ứng thành trọng tâm của tam giác A’B’C’.