Chương III – HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Bài 1. Phương trình bậc nhất hai ẩn.

A. Kiến thức cơ bản:

1. Khái niệm:

Phương trình bậc nhất hai ẩn x, y là hệ thức dạng:

ax + by = c                  (1)

Trong đó a, b và cc là các số đã biết (a ≠ b hoặc b ≠ 0).

2. Tập hợp nghiệm của phương trình:

a) Một nghiệm của phương trình (1) là một cặp số

(x₀, y₀) sao cho ax₀ + by₀ = c.

b) Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm. Tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c,

kí hiệu là (d).

–  Nếu a ≠ 0 và b ≠ 0 thì công thức nghiệm là:

$\{\begin{array}{ccc}x\in R& & \\ y=\frac{c-a\mathrm{x/}}{b}\end{array}$ hoặc $\{\begin{array}{c}x=\frac{c-b\mathrm{y/a}}{}\end{array}$

Khi đó đường thẳng (d) cắt cả hai trục tọa độ.

– Nếu a = 0, b ≠ 0 thì công thức nghiệm là:

$\{\begin{array}{ccc}x\in R& & \\ y=\frac{\mathrm{c/}}{b}\end{array}$ và (d) // Ox

– Nếu a ≠ 0, b = 0 thì công thức nghiệm là:

$\{\begin{array}{ccc}x=\frac{\mathrm{c/}}{\mathrm{a\; ,}}& & \\ y\in R& & \end{array}$ và (d) // Oy.

B Bài tập và lời giải 

1. Trong các cặp số $(-2;1)$, $(0;2),$ $(-1;0)$, $(1,5;3)$và $(4;-3)$, cặp số nào là nghiệm của phương trình:

a) $5x+4y=8$?                            b) $3x+5y=-3$ ?

Giải:

a) Thay từng cặp số đã cho vào phương trình $5x+4y=8$, ta được:

+) $5(-2)+4.1=-10+4=-6\ne 8$nên cặp số $(-2;1)$ không là nghiệm của phương trình.

+) $5.0+4.2=8$nên cặp số $(0;2)$là nghiệm của phương trình.

+) $5.(-1)+4.0=-5\ne 8$nên $(-1;0)$ không là nghiệm của phương trình.

+) $5.1,5+4.3=7,5+12=19,5\ne 8$ nên $(1,5;3)$không là nghiệm của phương trình.

+) $5.4+4.(-3)=20-12=8$ nên $(4;-3)$là nghiệm của phương trình.

Vậy có hai cặp số $(0;2)$ và $(4;-3)$là nghiệm của phương trình $5x+4y=8$.

b)Thay từng cặp số đã cho vào phương trình $3x+5y=-3$ ta được:

+) $3.(-2)+5.1=-6+5=-1\ne -3$nên $(-2;1)$ không là nghiệm của phương trình.

+) $3.0+5.2=10\ne -3$nên $(0;2)$ không là nghiệm của phương trình.

+) $3.(-1)+5.0=-3$ nên (-1; 0) là nghiệm của phương trình.

+) $3.1,5+5.3=4,5+15=19,5\ne -3$ nên $(1,5;3)$ không là nghiệm của phương trình.

+) $3.4+5.(-3)=12-15=-3$ nên $(4;-3)$là nghiệm của phương trình.

Vậy có hai cặp số $(-1;0)$ và $(4;-3)$ là nghiệm của phương trình $3x+5y=-3$

2. Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:

a) $3x-y=2$                                     b)$x+5y=3$

c) $4x-3y=-1$                              d) $x+5y=0$;

e) $4x+0y=-2$;                                  f) $0x+2y=5$.

Bài giải:

a) Ta có phương trình $3x-y=2$ (1)          

          (1) ⇔ $\{\begin{array}{c}x\in R\; ,\end{array}$y=3x−2

Ta được nghiệm tổng quát của phương trình là: $(x;3x-2)$

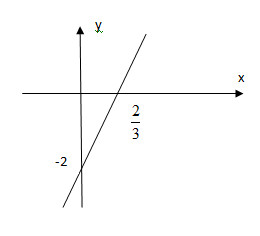
* Vẽ đưởng thẳng biểu diễn tập nghiệm của phương trình $y=3x-2$

Cho $x=0\Rightarrow y=-2$ ta được $A(0;-2)$

Cho $y=0\Rightarrow x=\frac{2}{3}$ ta được $B(\frac{2}{3};0)$.

Biểu diễn cặp số $A(0;-2)$ và $B(\frac{2}{3};\mathrm{0)}$trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình $3x-y=2$.

b)Ta có phương trình $x+5y=3$   (2)

(2) ⇔ $\{\begin{array}{ccc}x=-5y+\mathrm{3\; ,}& & \\ y\in R\end{array}$

Ta được nghiệm tổng quát của phương trình là (-5y + 3; y).

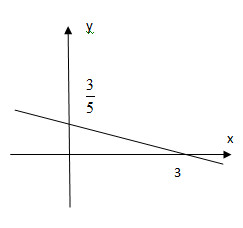
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình $x=-5y+3$:

+) Cho  $x=0\Rightarrow y=\frac{3}{5}$ta được $A\left(0;\frac{3}{5}\right)$

+) Cho  ta được $B\left(3;0\right)$.

Biểu diễn cặp số $A\left(0;\frac{3}{5}\right)$, $B\left(3;0\right)$ trên hệ trục toa độ và đường thẳng AB chính là tập nghiệm của phương trình.

     

c) Ta có phương trình $4x-3y=-1$    (3)

   (3) ⇔ $\{\begin{array}{ccc}x\in \mathrm{R\; ,}& & \\ y=\frac{4}{3}x+\frac{1}{3}\end{array}$

Ta được nghiệm tổng quát của phương trình là: $\left(x;\frac{4}{3}x+\frac{1}{3}\right)$

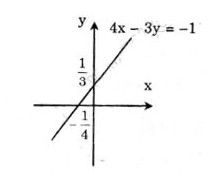
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình $4x-3y=-1$

+) Cho $x=0\Rightarrow y=\frac{1}{3}$ ta được $A\left(0;\frac{1}{3}\right)$

+) Cho $y=0\Rightarrow x=-\frac{1}{4}$ ta được $B\left(-\frac{1}{4};0\right)$

Biểu diễn cặp số $A(0;\frac{1}{3})$ và ; 0) trên hệ tọa độ và đường thẳng AB chính là tập nghiệm của phương trình $4x-3y=-1$.

 

 

d)Ta có phương trình $x+5y=0$    (4)  

(4) ⇔ $\{\begin{array}{ccc}x=-5\mathrm{y\; ,}& & \\ y\in R\end{array}$

Ta được nghiệm tổng quát của phương trình là: $(-5y;y)$

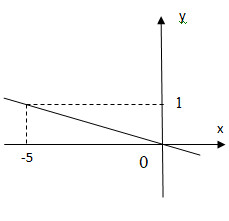
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình $x+5y=0$

+) Cho  ta được $O\left(0;0\right)$

+) Cho $y=1\Rightarrow x=-5$ ta được $A\left(-5;1\right)$

Biểu diễn cặp số $O(0;0)$và $A(-5;1)$ trên hệ tọa độ và đường thẳng OA chính là tập nghiệm của phương trình $x+5y=0$.

  

 

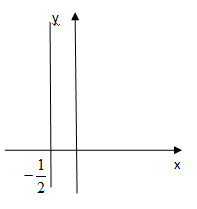
e) Ta có phương trình $4x+0y=-2$      (5)

(5)   ⇔ $\{\begin{array}{ccc}x=-\frac{1}{\mathrm{2\; ,}}& & \\ y\in R\end{array}$

Ta được nghiệm tổng quát của phương trình là: $\left(-\frac{1}{2};y\right)$

Tập nghiệm là đường thẳng $x=-\frac{1}{2}$, qua $A(-\frac{1}{2};0)$và song song với trục tung.

  

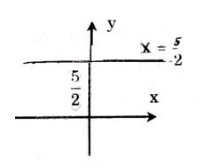
f) 0x + 2y = 5       (6)

 (6) ⇔ $\{\begin{array}{ccc}x\in \mathrm{R\; ,}& & \\ y=\frac{5}{2}\end{array}$

Ta được nghiệm tổng quát của phương trình là $\left(x;\frac{5}{2}\right)$

Tập nghiệm là đường thẳng $y=\frac{5}{2}$qua  và song song với trục hoành.