Chương 4: Giới hạn (giới hạn dãy số, giới hạn hàm số, hàm số liên tục)

Lý thuyết về giới hạn: giới hạn dãy số, giới hạn hàm số, hàm số liên tục

Bài 1: Giới hạn của dãy số

Tóm tắt lý thuyết giới hạn dãy số

1. Giới hạn hữu hạn và giới hạn vô cực

a). Giới hạn hữu hạn

b). Giới hạn vô cực

 2. Các giới hạn đặc biệt

3. Định lí về giới hạn hữu hạn

a)Nếu limu_n = a và limv_n = b, thì:

b). Nếu u_n >0, và limu_n = a, thì :

4. Định lí liên hệ giữa giới hạn hữu hạn và giới hạn vô cực.

a) Nếu lim u_n = a và lim v_n = ± ∞ thì lim  = 0.

b)  Nếu lim u_n = a > 0, lim v_n = 0 và v_n > 0 với mọi n thì lim  = +∞

c) Nếu lim u_n = +∞ và lim v_n = a > 0 thì lim (u_{n .}  v_n) = +∞.

5. Cấp số nhân lùi vô hạn

+ Cấp số nhân lùi vô hạn là cấp số nhân vô hạn có công bội q thỏa mãn |q| <1.

+) Công thức tính tổng S của cấp số lùi vô hạn (u_n):

Bài 2: Giới hạn của hàm số

+) Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K\{x0}.

limx→x0 f(x)=L khi và chỉ khi với dãy số (xn) bất kì, xn ∈ K \{x0} và xn → x0, ta có:
limf(xn)=L.

2. Giới hạn vô cực

3. Các giới hạn đặc biệt

4. Định lí về giới hạn hữu hạn

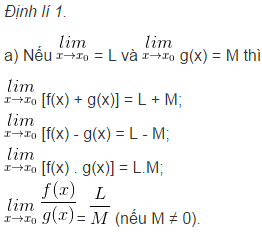
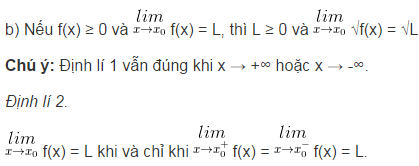
5. Quy tắc về giới hạn vô cực

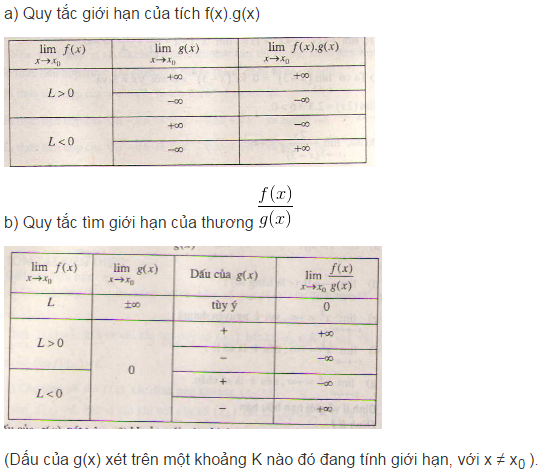
Bài 3: Hàm số liên tục

A. Tóm tắt lý thuyết

1) Hàm số liên tục tại một điểm 

Hàm số liên tục: Giả sử hàm số y=f(x) xác định trên (a;b) và $x_0\in (a;b)$

Hàm số y=f(x) liên tục tại $x_0\iff {lim}_{x\to x_0}f\left(x\right)=f\left(x_0\right)$

Hàm số không liên tục tại $x_0$ được gọi là gián đoạn tại $x_0$.

2) Hàm số liên tục trên một khoảng, một đoạn

Hàm số y=f(x) xác định trên (a;b). f(x) liên tục trên khoảng (a;b) khi và chỉ khi f(x) liên tục tại mọi điểm thuộc (a;b).

Hàm số y=f(x) xác định trên $\left[a;b\right]$. f(x) liên tục trên $\left[a;b\right]$  khi và chỉ khi f(x) liên tục tại mọi điểm thuộc (a;b) và 

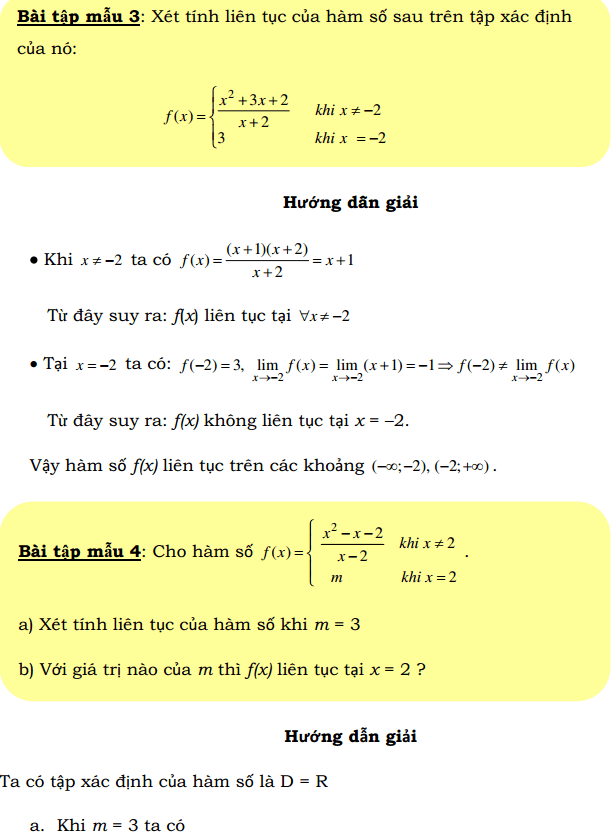
Ôn tập chương 4