Đề chuyên sư phạm và đáp án chi tiết lần 3 – 2017
Đây là đề Toán khá hay các em học sinh có thể tham khảo.
ĐÁP ÁN CHI TIẾT CÓ TRONG KHÓA LUYỆN ĐỀ: LINK ĐĂNG KÍ KHÓA SIÊU LUYỆN ĐỀ
LƯU Ý CÁC BẠN ĐÃ MUA SÁCH TÂM PHÁP THẾ ANH ĐƯỢC TẶNG KÈM BỘ ĐỀ CHUYÊN NÀY





Đề CHUYÊN SƯ PHẠM HÀ NỘI
Câu 1: (Hàm số – Chuyên Sư phạm – Hà Nội) Gọi , là các điểm cực tiểu của đồ thị hàm số . Diện tích của tam giác (với là gốc tọa độ) bằng.
Câu 2: (Hàm số – Chuyên Sư phạm – Hà Nội) Tìm tất cả các giá trị thực của tham số để đồ thị hàm số sau có hai điểm cực trị cách đều trục tung
Câu 3: (Hình không gian – Chuyên Sư phạm – Hà Nội) Cho hình chóp có đáy là hình vuông cạnh , mặt bên là tam giác đều, mặt bên là tam giác vuông cân đỉnh . Thể tích khối chóp là
Câu 4: (Hình không gian – Chuyên Sư phạm – Hà Nội) Cho hình lăng trụ đứng có tất cả các cạnh bằng Thể tích khối tứ diện là
Câu 5: (Hàm số – Chuyên Sư phạm – Hà Nội) Phương trình có bao nhiêu nghiệm thực phân biệt
Câu 6: (Hình không gian – Chuyên Sư phạm – Hà Nội) Cho hình trụ có các đáy là hai hình tròn tâm và , bán kính đáy bằng chiều cao và bằng . Trên đường tròn đáy tâm lấy điểm , trên đường tròn đáy tâm lấy điểm , sao cho . Thể tích khối tứ diện là
Câu 7: (Hàm số – Chuyên Sư phạm – Hà Nội) Tìm hàm số dưới đây, biết rằng đồ thị hàm số cắt trục tung tại điểm và đồ thị có giao điểm hai đường tiệm cận là .
Câu 8: (Hàm số – Chuyên Sư phạm – Hà Nội) Tập hợp nghiệm của hệ bất phương trình là
Câu 9: (Oxyz – Chuyên Sư phạm – Hà Nội) Trong không gian với hệ tọa độ , cho và các điểm , , thuộc các trục , , sao cho hình chóp có các cạnh , , đôi một vuông góc với nhau. Tính thể tích khối chóp .
Câu 10: (Hình không gian – Chuyên Sư phạm – Hà Nội) Cần xẻ một khúc gỗ hình trụ có đường kính và chiều dài thành một cái xà hình hộp chữ nhật có cùng chiều dài. Lượng gỗ bỏ đi tối thiểu xấp xỉ là
Câu 11: (Nguyên hàm tích phân – Chuyên Sư phạm – Hà Nội) Đạo hàm của hàm số là
Câu 12: (Hàm số – Chuyên Sư phạm – Hà Nội) Tìm tất cả các giá trị thực của tham số để đồ thị hàm số có đúng hai đường tiệm cận ngang.
Câu 13: (Hình không gian – Chuyên Sư phạm – Hà Nội) Một đống cát hình nón cụt có chiều cao , bán kính đáy lớn , bán kính đáy nhỏ . Thể tích đống cát xấp xỉ
.Câu 14: (Hàm số – Chuyên Sư phạm – Hà Nội) Tất cả đường tiệm cận đứng của đồ thị hàm số
Câu 15: (Hình không gian – Chuyên Sư phạm – Hà Nội) Cho hình hộp có tất cả các cạnh bằng và , . Thể tích hình hộp là
Câu 16: (Hình Oxyz – Chuyên Sư phạm – Hà Nội) Trong không gian với hệ tọa độ , cho hai đường thẳng , . Đường thẳng đi qua cắt , tại và . Độ dài là
Câu 17: (Hình Oxyz – Chuyên Sư phạm – Hà Nội) Cho hàm số Hãy tính
Câu 18: (Hình Oxyz – Chuyên Sư phạm – Hà Nội) Trong không gian với hệ tọa độ , cho mặt cầu Tiếp diện của tại điểm có phương trình là
Câu 19: (Hình không gian – Chuyên Sư phạm – Hà Nội) Cho hình nón có đỉnh là , đường tròn đáy là có bán kính góc ở đỉnh của hình nón là Hình chóp đều có các đỉnh thuộc đường tròn có thể tích là
Câu 20: (Hàm số – Chuyên Sư phạm – Hà Nội) Tất cả các đường tiệm cận ngang của đồ thị hàm số là
Câu 20: (Mũ Logarit – Chuyên Sư phạm – Hà Nội)Gọi , là các nghiệm của phương trình Khi đó tích , bằng
Câu 21: (Hàm số – Chuyên Sư phạm – Hà Nội) Tìm tất các những điểm thuộc đồ thị hàm số có khoảng cách đến đường tiệm cận ngang của đồ thị bằng
Câu 22: (Nguyên hàm – Tích phân – Chuyên Sư phạm – Hà Nội) Cho hàm số Hãy tính
Câu 23 (Hình không gian – Chuyên Sư phạm – Hà Nội)Hình chóp đều có cạnh đáy bằng góc giữa cạnh bên và mặt đáy bằng có thể tích là
Câu 25 (Hình Oxyz – Chuyên Sư phạm – Hà Nội) Trong không gian với hệ tọa độ cho ba điểm ; ; và mặt phẳng . Điểm thuộc sao cho . Thể tích khối chóp là
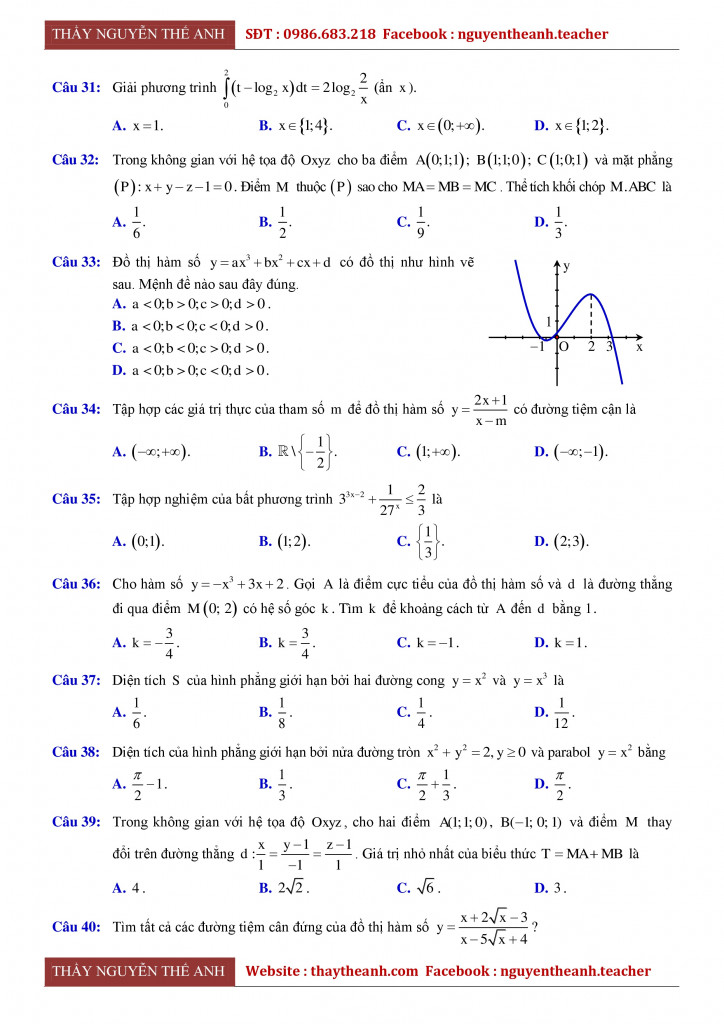
Câu 26 (Hàm số – Chuyên Sư phạm – Hà Nội) Đồ thị hàm số có đồ thị như hình vẽ sau. Mệnh đề nào sau đây đúng.
Câu 25 (Hàm số – Chuyên Sư phạm – Hà Nội) Tập hợp các giá trị thực của tham số để đồ thị hàm số có đường tiệm cận là
Câu 26 (Hàm số – Chuyên Sư phạm – Hà Nội) Cho hàm số . Gọi là điểm cực tiểu của đồ thị hàm số và là đường thẳng đi qua điểm có hệ số góc . Tìm để khoảng cách từ đến bằng .
Câu 27 (Tích phân nguyên hàm – Chuyên Sư phạm – Hà Nội) Diện tích của hình phẳng giới hạn bởi nửa đường tròn và parabol bằng
Câu 28 (Hình Oxyz – Chuyên Sư phạm – Hà Nội) Trong không gian với hệ tọa độ , cho hai điểm , và điểm thay đổi trên đường thẳng . Giá trị nhỏ nhất của biểu thức là
Câu 29 (Hàm số – Chuyên Sư phạm – Hà Nội) Cho hàm số khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng
Câu 30 (Oxyz – Chuyên Sư phạm – Hà Nội) Trong không gian với hệ tọa độ , cho hai điểm , . Đường thẳng cắt mặt phẳng tọa độ tại điểm . Giá trị của biểu thức là
Câu 30 (Nguyên hàm tích phân – Chuyên Sư phạm – Hà Nội) tất cả các giá trị thực của tham số để bất phương trình sau đây nghiệm đúng với mọi giá trị thực của .
Câu 30 (Hình không gian – Chuyên Sư phạm – Hà Nội) Cho lăng trụ đứng có đáy là tam giác vuông cân đỉnh , , . Diện tích mặt cầu ngoại tiếp tứ diện là
Câu 31 (Hình không gian – Chuyên Sư phạm – Hà Nội) Trong không gian với hệ tọa độ , cho hai điểm , và mặt cầu . Mặt phẳng đi qua , và cắt mặt cầu theo giao tuyến là đường tròn có bán kính lớn nhất có phương trình là
Câu 33 (Hàm số – Chuyên Sư phạm – Hà Nội) Tìm tất cả các giá trị thực của tham số để hệ phương trình có nghiệm thực
Câu 32 (Hình không gian – Chuyên Sư phạm – Hà Nội) Tập hợp nghiệm của phương trình (ẩn ) là
Câu 33 (Số phức – Chuyên Sư phạm – Hà Nội) Cho hai số phức , thỏa mãn . Khi đó bằng