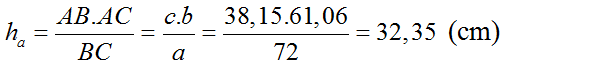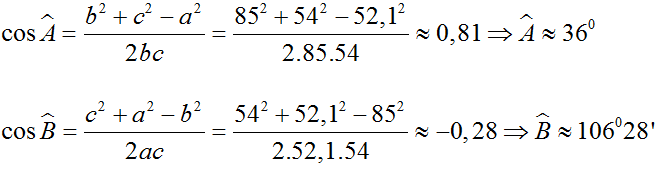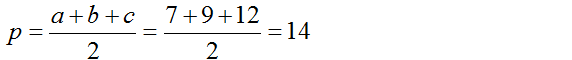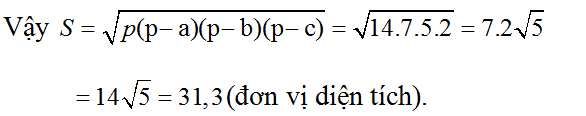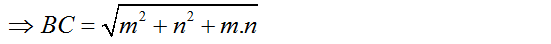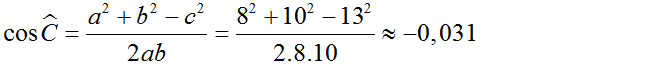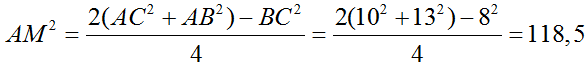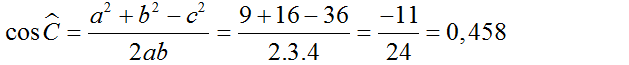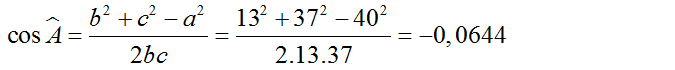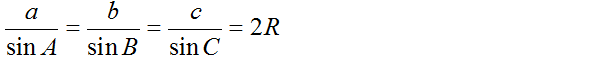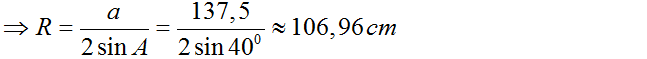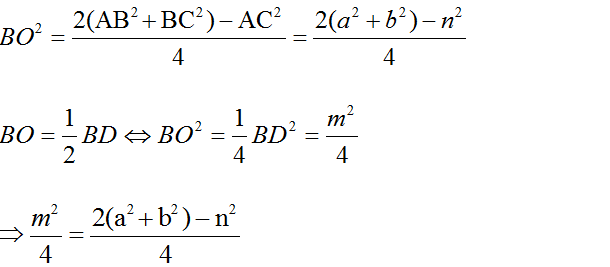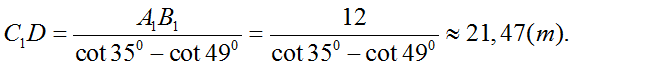Lý thuyết và bài tập các hệ thức lượng trong tam giác và giải tam giác

A. Lý thuyết các hệ thức lượng trong tam giác và giải tam giác

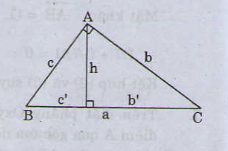
Nhắc lại hệ thức lượng trong tam giác vuông.

Cho tam giác ABC vuông góc tại đỉnh A (A= 90⁰), ta có:

1. b²= a.b’;  c² = a.c’

2. Định lý Pitago : a² = b² + c²

3. a.h = b.c

4. h² = b’.c’

5.  

1. Định lý cosin

Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.

Ta có các hệ thức sau:   a² = b² + c² – 2bc.cosA   (1)

                                   b² = a² + c² – 2bc.cosB   (2)

                                   c² = a² + b² – 2bc.cosC   (3)

 

Áp dụng: Tính độ dài đường trung tuyến của tam giác:

Cho tam giác ABC có các cạnh BC = a, CA = b và AB = c. Gọi m_a, m_b và m_c là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác. Ta có

 

2. Định lí sin

Định lí: Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là

a/sinA=b/sinB=c/sinC= 2R

với R là bán kính đường tròn ngoại tiếp tam giác 

Công thức tính diện tích tam giác:

Ta kí hiệu h_a, h_b và h_c là các đường cao của tam giác ABC lần lượt vẽ từ các đình A, B, C và S là diện tích tam giác đó.

Diện tích S của tam giác ABC được tính theo một trong các công thức sau

S = ab sinC/2=  bc sinA/2 = ca sinB/2                               (1)

S = abc/4R                                                                             (2)

S = pr                                                                                   (3)

S = công thức  Hê – rông) (4)

3. Giải tam giác và ứng dụng vào việc đo đạc

Giải tam giác : Giải tam giác là tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.

Muốn giải tam giác ta cần tìm mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.

Các bài toán về giải tam giác: Có 3 bài toán cơ bản về giải tam giác:

a) Giải tam giác khi biết một cạnh và hai góc.

Đối với bài toán này ta sử dụng định lí sin để tính cạnh còn lại

b) Giải tam giác khi biết hai cạnh và góc xen giữa

Đối với bài toán này ta sử dụng định lí cosin để tính cạnh thứ ba

c) Giải tam giác khi biết ba cạnh

Đối với bài toán này ta sử dụng định lí cosin để tính góc 

 

Chú ý: 

1. Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)

2. Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.

[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]

B. Lý thuyết các hệ thức lượng trong tam giác và giải tam giác

Bài 1 trang 59 sgk hình học 10

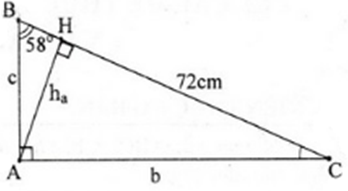
Bài 1 (trang 59 SGK Hình học 10): Cho tam giác ABC vuông tại A, ∠B = 58^o và cạnh a = 72cm. Tính ∠C, cạnh b và đường cao h.

Lời giải:

– Ta có: ∠C = 90^o – ∠B = 90^o – 58^o = 32^o

– Ta có: b = BC.sin58^o = a.sin58^o = 61,06 (cm)

– Ta có: c = BC.cos58^o = a.cos58^o = 38,15 (cm)

Do đó:

1. Cho tam giác ABC vuông tại A,  = 58⁰

và cạnh a = 72 cm. Tính , cạnh b, cạnh c và đường cao h_a.

Hướng dẫn:

 

 = 32⁰; b = a.cos32⁰     =>   b ≈ 61,06cm;         c =  a.sin32⁰ ≈ 38,15cm

      h_a =                    =>   h_a ≈ 32,35cm

Bài 2 trang 59 sgk hình học 10

Bài 2 (trang 59 SGK Hình học 10): Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc ∠A, ∠B, ∠C.

Lời giải:

=> ∠C = 180^o – ∠A – ∠B = 37^o32′

2. Cho tam giác ABC biết các cạnh a = 52, 1cm; b = 85cm và c = 54cm. Tính các góc , 

Hướng dẫn:

Từ định lí cosin a² = b² + c² – 2bc. cosA

ta suy ra    cos A = = 

=> cosA  ≈ 0,8089  =>  36⁰ 

Tương tự, ta tính được     ≈  106⁰ 28’ ;            ≈  37⁰ 32’.

Bài 3 trang 59 sgk hình học 10

Bài 3 (trang 59 SGK Hình học 10): Cho tam giác ABC có ∠A = 120^o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc ∠B, ∠C của tam giác đó.

Lời giải:

– Ta có: a² = b² + c² – 2bccos∠A

= 8² + 5² – 2.8.5.cos120^o

=> a = √129 = 11,36 (cm)

=> ∠B = 37^o34′

=> ∠C = 180^o – (∠A + ∠B)

= 180^o – (120^o + 37^o34′) = 22^o26′

3. Cho tam giác ABC có  = 120⁰ cạnh b = 8cm và c = 5cm. Tính cạnh a, và góc    của tam giác đó.

Hướng dẫn giải:

Ta có   

 a² = 8²  + 5² – 2.8.5 cos 120⁰ = 64 + 25 + 40 = 129

=> a = √129  ≈ 11, 36cm

 Ta có thể tính góc B theo định lí cosin

 cosB =  =  ≈  0,7936 =>  = 37⁰48’

Ta cũng có thể tính góc B theo định lí sin :

cosB = =  => sinB  ≈  0,6085 =>  = 37⁰48’

Tính C từ  = 180⁰– ( +    =>  ≈ 22⁰12’

Bài 4 trang 59 sgk hình học 10

Bài 4 (trang 59 SGK Hình học 10): Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.

Lời giải:

Ta có:

    p – a = 7

    p – b = 5

    p – c = 2

4. Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.

Hướng dẫn:

Ta có 2p = 7 + 9 + 12  => p = 14

p – a = 14 – 7 = 7

p – b = 14 – 9 = 5

p – c = 12 – 12 = 2

Áp dụng công thức Hê ron:

S =  = = 14√5 (dvdt)

Bài 5 trang 59 sgk hình học 10

Bài 5 (trang 59 SGK Hình học 10): Cho tam giác ABC có ∠A = 120^o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.

Lời giải:

Ta có: BC² = AC² + AB² – 2.AB.AC.cos∠A

    = m² + n² – 2.m.n.cos120^o

    = m² + n² + mn

5. Tam giác ABC có  = 120⁰. Tính cạnh BC cho biết cạnh AC = m và AB = n.

 Hướng dẫn:

Ta có: BC² = AC² + AB² – 2AB.AC. cos120⁰

=> BC² = m² + n² – 2m.n (

=> BC² = m² + n² + m.n

=> BC = 

Bài 6 trang 59 sgk hình học 10

Bài 6 (trang 59 SGK Hình học 10): Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.

a) Tam giác đó có góc tù không?

b) Tính độ dài trung tuyến MA của tam giác ABC đó.

Lời giải:

a) Ta có:

=> ∠C = 91^o47′

Vậy trong tam giác có ∠C là góc tù.

=> AM = √118,5 = 10,89

6. Tam giác ABC có các cạnh a = 8cm, b = 10cm, c = 13cm

a) Tam giác đó có góc tù không? 

b) Tính độ dài đường trung tuyến MA của tam giác ABC đó.

Hướng dẫn:

a) Xét tổng  a^{2 +} b²  – c² = 8^{2 +} 10²  – 13² = -5 < 0 

Vậy tam giác này có góc C tù

cos C = = ≈ -0, 3125   =>   =  91⁰47’

b) Áp dụng công thức tính đường trung tuyến, ta tính được AM ≈ 10,89cm

Bài 7 (trang 59 SGK Hình học 10): Tính góc lớn nhất của tam giác ABC biết:

a) Các cạnh a = 3cm, b = 4cm và c = 6cm;

b) Các cạnh a = 40cm, b = 13cm, c = 37cm.

Lời giải:

a) Cạnh c = 6cm lớn nhất suy ra là góc lớn nhất.

Vậy ∠C = 117^o16′

Vậy ∠A = 93^o41′

Tính góc lớn nhất của tam giác ABC biết:

a) Các cạnh a = 3cm, b = 4cm, c = 6cm

b) Các cạnh a = 40cm, b = 13cm, c = 37cm

Hướng dẫn:

Ta biết trong tam giác thì đối diện với cạnh lớn nhất là góc lớn nhất, vậy trong câu a) góc lớn nhất là góc C còn trong câu b) góc lớn nhất là góc A

a) cos = ≈  -0,4583     => =  117⁰16’

b)cos  = =             =>  = 93⁰41’

 

Bài 8 trang 59 sgk hình học 10

Bài 8 (trang 59 SGK Hình học 10): Cho tam giác ABC biết cạnh a = 137,5cm, ∠B = 83^o và ∠C = 57^o. Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.

Lời giải:

Ta có: ∠A = 180^o – (∠B + ∠C) = 180^o – (83^o + 57^o) = 40^o

Áp dụng định lí sin ta có:

Từ đó suy ra:

=> b = 2R.sin B = 2.106,96.sin83^o = 212,33 cm

=> c = 2R.sin C = 2.106,96.sin57^o = 179,41 cm

Cho tam giác ABC biết cạnh a = 137,5cm;  = 83^{0 ;}  = 57⁰. Tính góc A, cạnh b và c của tam giác.

Hướng dẫn:

Ta có: = 180⁰ – ( + ) = 40⁰

Áp dụng định lí sin :

                            ta có:

                              b =  ≈ 212,32cm   

                              c = ≈ 179,40cm

Bài 9 trang 59 sgk hình học 10

Bài 9 (trang 59 SGK Hình học 10): Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m² + n² = 2(a² + b²).

Lời giải:

Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD, đồng thời BO là trung tuyến của ΔABC.

Suy ra:

⇔ m² + n² = 2(a² + b²) (đpcm)

Cho hình bình hành ABCD có AB = a, BC = b ,BD = m, và AC = n. Chứng minh rằng 

 m² + n²  = 2(a²  + b² )

Hướng dẫn:

Áp dụng định lí về đường trung tuyến:

OA² =  – 

Thay OA =  , AB = a

AD = BC = b và BD = m => dpcm

Bài 10 trang 60 sgk hình học 10

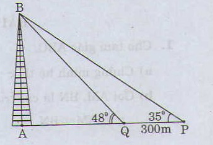
Bài 10 (trang 60 SGK Hình học 10): Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các góc ∠BPA = 35^o và ∠BQA = 48^o. Tính chiều cao của tháp.

Lời giải:

ΔAPB vuông tại A có ∠APB = 35^o

=> AP = ABcot35^o     (1)

ΔAQB vuông tại A có ∠AQB = 35^o

=> AQ = ABcot48^o     (2)

Từ (1) và (2) suy ra:

PQ = AP – AQ = AB(cot35^o – cot48^o)

Hai chiếc tàu thủy P và Q cách nhau 300m.TỪ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc   = 35⁰  = 48⁰

Tính chiều cao của tháp.

Hướng dẫn :

Ta có: AQ = ABcot48⁰ 

AP = ABcot35⁰ 

QP = AB(cot35⁰ – cot48⁰) 

=> AB =  ≈ 

Tính được AB ≈ 568,50m

Bài 11 trang 60 sgk hình học 10

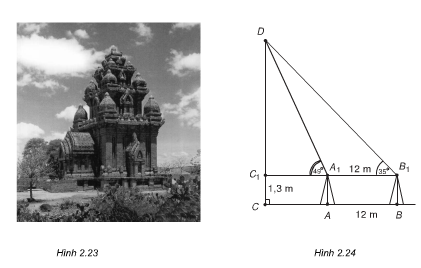
Bài 11 (trang 60 SGK Hình học 10): Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A₁, B₁ cùng thẳng hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được ∠DA₁C₁ = 49^o và ∠DB₁C₁ = 35^o. Tính chiều cao CD của tháp đó.

Lời giải:

Ta có: A₁B₁ = AB = 12 m

Xét ΔDC₁A₁ có: C₁A₁ = C₁D.cot49^o

Xét ΔDC₁B₁ có: C₁B₁ = C₁D.cot35^o

Mà A₁B₁ = C₁B₁ – C₁A₁ = C₁D.cot35^o – C₁D.cot49^o

        = C₁D.(cot35^o – cot49^o)

=> Chiều cao CD của tháp là:

        CD = 1,3 + 21,47 = 22,77 m

Muốn đo chiều cao của tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12cm cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của giác kế có chiều cao h = 1,3cm. Gọi D là đỉnh tháp và hai điểm A_1, B₁, cùng thẳng  hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được = 49⁰ và   = 35^0. 

hướng dẫn giải:

Ta có: Chiều cao của tháp DC = DC₁ + C₁C = 1,3 + DC₁ 

=> DC = 1,3 +  

=> DC ≈ 22,8m