Lý thuyết và bài tập giá trị lượng giác của một cung
Lý thuyết giá trị lượng giác của một cung
1. Định nghĩa
Trên đường tròn lượng giác cho cung có số đo sđ = α thì:
+ Tung độ của M gọi là sin của α, kí hiệu sinα: = sinα
+ Hoành độ của M gọi là cosin của α, kí hiệu là cosα: = cosα
+ Nếu cosα # 0, ta gọi là tang của α, kí hiệu tanα là tỉ số: = tanα
+ Nếu sinα # 0, ta gọi là cotang của α, kí hiệu là = cotα
Ghi chú: Vì sđ = sđ (OA, OM) nên định nghĩa các giá trị lượng giác của cung lượng giác α cũng là giá trị lượng giác của góc lượng giác α.
2. Hệ quả
a) -1 ≤ sinα ≤ 1, -1 ≤ cosα ≤ 1 ∀α thuộc R
sin(α + k2π) = sinα ∀k thuộc Z
cos(α + k2π) = cosα ∀k thuộc Z
b) tanα xác định với mọi α # + kπ, ∀k thuộc Z
cotα xác định với mọi α # kπ, ∀k thuộc Z
tan(α + kπ) = tanα ∀k thuộc Z
cot(α + kπ) = cotα ∀k thuộc Z
c) Bảng xác định dấu của các giá trị lượng giác
d) Các hệ thức lượng giác cơ bản:
sin2α + cos2α = 1; tanα.cotα = 1
1 + tan2α = 1 + cot2α =
3. Giá trị lượng giác của các cung có liên quan đặc biệt
a) Cung đối nhau: α và (-α)
sin(-α) = -sinα tan(-α) = -tanα
cos(-α) = cosα cot(-α) = -cotα
b) Cung bù nhau: α và π – α
sin(π – α) = sinα tan(π – α) = -tanα
cos(π – α) = -cosα cot(π – α) = -cotα
c) Cung hơn nhau π: α và π + α
sin(π + α) = -sinα tan(π + α) = tanα
cos(π + α) = -cosα cot(π + α) = cotα
d) Cung phụ nhau: α và (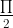 – α)
– α)
sin( – α) = cosα tan(
– α) = cosα
cos( – α) = sinα cot(
– α) = tanα
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]
Bài tập giá trị lượng giác của một cung
Bài 1 trang 148 sgk đại số 10
Bài 1. Có cung α nào mà sinα nhận các giá trị tương ứng sau đây không?
a) -0,7; b) c) -√2; d)
Hướng dẫn giải:
a) -1 ≤ -0,7 ≤ 1. Có cung α mà sin α = -0,7
b) > 1. Không có cung α có sin nhận giá trị
c) Không. Vì -√2 < -1
d) Không. Vì > 1
Bài 2 trang 148 sgk đại số 10
Bài 2. Các đẳng thức sau có thể đồng thời xảy ra không?
a) sinα = và cosα =
;
b) sinα = – và cosα =
Hướng dẫn giải:
a) Không. Bởi vì
< 1
b) Có thể đồng thời xảy ra, vì = 1
c) Không. Lí do như câu a
Bài 3 trang 148 sgk đại số 10
Bài 3. Cho 0 < α < . Xác định dấu của các giá trị lượng giác
a) sin(α – π); b) cos( – α)
c) tan(α + π); d) cot(α + )
Hướng dẫn giải:
Với 0 < α < :
a) sin(α – π) < 0; b) cos( – α) < 0;
c) tan(α + π) > 0; d) cot(α + ) < 0
Bài 4 trang 148 sgk đại số 10
Bài 4. Tính các giá trị lượng giác của góc α, nếu:
a) cosα = và 0 < α <
; b) sinα = -0,7 và π < α <
;
c) tan α = và
< α < π; d) cotα = -3 và
< α < 2π.
Hướng dẫn giải:
a) Do 0 < α < nên sinα > 0, tanα > 0, cotα > 0
sinα =
cotα = ; tanα =
b) π < α < nên sinα < 0, cosα < 0, tanα > 0, cotα > 0
cosα = -√(1 – sin2 α) = -√(1 – 0,49) = -√0,51 ≈ -0,7141
tanα ≈ 0,9802; cotα ≈ 1,0202.
c) < α < π nên sinα > 0, cosα < 0, tanα < 0, cotα < 0
cosα = ≈ -0,4229.
sinα =
cotα = –
d) Vì < α < 2π nên sinα < 0, cosα > 0, tanα < 0, cotα < 0
Ta có: tanα =
cosα =
Bài 5 trang 148 sgk đại số 10
Bài 5. Tính α, biết:
a) cosα = 1; b) cosα = -1
c) cosα = 0; d) sinα = 1
e) sinα = -1; f) sinα = 0,
Hướng dẫn giải:
a) α = k2π, k thuộc Z
b) α = (2k + 1)π, k thuộc Z
c) α = + kπ, k thuộc Z
d) α = + k2π, k thuộc Z
e) α = + k2π, k thuộc Z
f) α = kπ, k thuộc Z
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]