NGUYÊN HÀM 2 ẨN, 3 ẨN

• Gồm có 2 phần lớn: Phần Tóm tắt lý thuyết và Phần bài tập.
• Phần tóm tắt lý thuyết gồm có định nghĩa, định lý, tính chất và các công thức nguyên hàm cơ bản. Thêm vào đó, còn có các link riêng của từng phần để các em học sinh và phụ huynh tìm hiểu kĩ hơn.
• Phần bài tập gồm các dạng bài tập của phần kiến thức về nguyên hàm 2 ẩn, 3 ẩn.
• Có thể thấy, các dạng bài của phần kiến thức về nguyên hàm 2 ẩn, 3 ẩn là các dạng bài khó và chống máy tính. Vì vậy ta phải thuộc lý thuyết, làm nhiều và thành thạo thì mới có thể có kết quả tốt trong các bài kiểm tra.

PHỤ HUYNH VÀ CÁC EM HỌC SINH CÓ THỂ TÌM HIỂU THÊM

Nguyên hàm – Lý thuyết và Bài tập

Các công thức nguyên hàm

Nguyên hàm hữu tỷ, vô tỷ

Nguyên hàm lượng giác

I. Tóm tắt nguyên hàm:

1. Định nghĩa:

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên (a;b)nếu F′(x)=f(x)

Ví dụ:

• Hàm số y=x² là nguyên hàm của hàm số y=2x trên R vì (x²)′=2x

2. Định lý:

1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

• Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C

3. Sự tồn tại của nguyên hàm:

• Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

4. Các tính chất:

5. Bảng công thức nguyên hàm của một số hàm số sơ cấp:

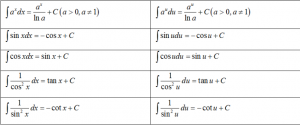
• Tìm hiểu thêm về các công thức nguyên hàm ( từ cơ bản đến nâng cao) ở đây.

II. Các bài tập về nguyên hàm 2 ẩn, 3 ẩn:

• 30 câu trắc nghiệm về kiến thức phần nguyên hàm 2 ẩn:

https://drive.google.com/file/d/1t56ZlR5hdgMuz_s6XBTw2XpRftkDjGzD/view?usp=sharing