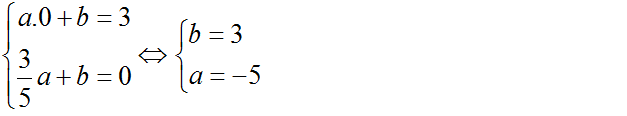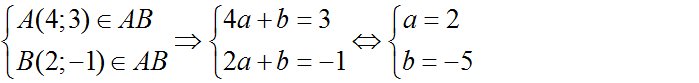Hàm số y = ax + b
Bài 1 (trang 41-42 SGK Đại số 10): Vẽ đồ thị của các hàm số:
a) y = 2x – 3;
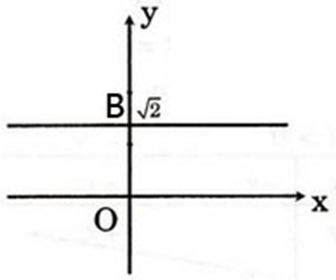
b) y = √2;
d) y = |x| – 1.
Lời giải:
a) y = 2x – 3
– Bảng giá trị:
| x | 0 | 1 |
| y | -3 | -1 |
Đồ thị hàm số y = 2x – 3 là đường thẳng qua hai điểm A(0; -3) và B(1 ; -1).
b) Đồ thị hàm số y = √2 là đường thẳng song song với trục hoành và qua điểm B(0 ; √2)
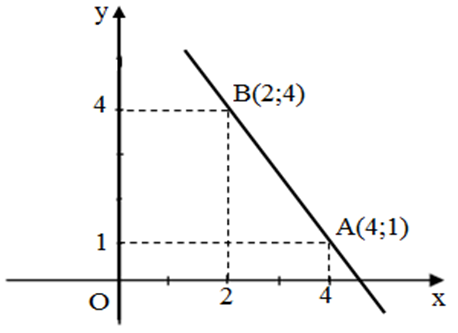
– Bảng giá trị
| x | 2 | 4 |
| y | 4 | 1 |
Đồ thị hàm số y là đường thẳng đi qua 2 điểm B(2 ; 4) và A(4 ;1).
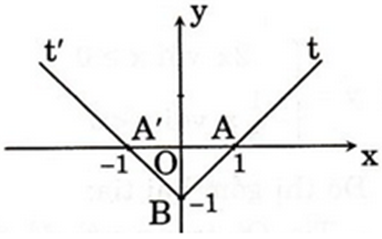
d) y = |x| – 1. Ta có:
– Bảng giá trị:
| x | -1 | 0 | 1 |
| y | 0 | -1 | 0 |
Đồ thị của hàm số trên là nửa đường thẳng BA’ với B(0; -1) và A'(-1; 0).
Đồ thị của y = |x| – 1 gồm hai tia Bt và Bt’.
Bài 2 (trang 42 SGK Đại số 10): Xác định a, b để đồ thị của hàm số y = ax + b đi qua các điểm
b) A(1; 2) và B(2; 1);
c) A(15; -3) và B(21; -3).
Lời giải:
Phương pháp:
– Điểm M(xo; yo) ∈ Δ ⇔ yo = axo + b (thay tọa độ điểm M vào phương trình hàm số)
– Giải hệ phương trình bậc nhất theo a và b.
a) Thay tọa độ A, B vào phương trình hàm số y = ax + b ta được:
=> Phương trình hàm số: y = – 5x + 3
b) Thay tọa độ A(1; 2), B(2; 1) vào phương trình hàm số y = ax + b ta được:
=> Phương trình hàm số: y = – x + 3
c) Thay tọa độ A(15; -3), B(21; -3) vào phương trình hàm số y = ax + b ta được:
=> Phương trình hàm số: y = – 3
Bài 3 (trang 42 SGK Đại số 10): Viết phương trình y = ax + b của các đường thẳng:
a) Đi qua hai điểm A(4;3), B(2 ; -1);
b) Đi qua điểm A(1 ; -1) và song song với Ox.
Lời giải:
a) Phương trình đường thẳng AB có dạng : y = ax + b (a, b là hằng số)
Ta có:
Vậy phương trình đường thẳng AB là y = 2x – 5.
b) Đường thẳng Δ cần tìm song song với Ox nên a = 0.
=> phương trình đường thẳng Δ có dạng y = b.
Mặt khác Δ đi qua A(1 ; -1) nên b = -1.
Vậy phương trình đường thẳng Δ là y = -1.
Bài 4 (trang 42 SGK Đại số 10): Vẽ đồ thị của các hàm số

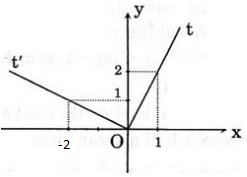
a)
– Vẽ đường thẳng y = 2x đi qua điểm (0; 0) và (1; 2). Trên đường thẳng này, ta giữ phần đường thẳng khi x ≥ 0. Đó là tia Ot.
– Vẽ đường thẳng y = -1/2 x đi qua điểm (0; 0) và (-2; 1). Trên đường thẳng này, ta giữ phần đường thẳng khi x < 0. Đó là tia Ot’
b)
– Vẽ đường thẳng y = x + 1 đi qua điểm A (1; 2) và B (2; 3). Trên đường thẳng này, ta giữ phần đường thẳng khi x ≥ 1. Đó là tia AB.
– Vẽ đường thẳng y = -2x + 4 đi qua điểm A (1; 2) và B’ (0; 4). Trên đường thẳng này, ta giữ phần đường thẳng khi x < 1. Đó là tia AB’.