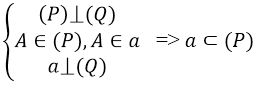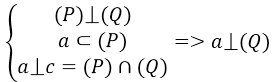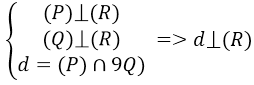Lý thuyết: Mặt phẳng vuông góc
1. Về kiến thức.
– Biết khái niệm góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳn đó. Lưu ý góc giữa hai mặt phẳng song song thì bằng 00.
– Biết khai niệm hai mặt phẳng vuông góc. Hai mặt phẳng được gọi là vuông góc khi góc giữa chúng bằng 900.
Điều kiện: hai mặt phẳng vuông góc khi và chỉ khi mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Hệ quả 1. Có hai mặt phẳng vuông góc. Nếu từ một điểm A của mặt phẳng (P) vẽ đường thẳng a vuông góc với mặt phẳng (Q) thì đường thẳng a sẽ thuộc mặt phẳng (P):
Hệ quả 2. Có hai mặt phẳng vuông góc, nếu một đường thẳng a thuộc mặt phẳng (P) mà vuông góc với giao tuyến thì nó sẽ vuôn góc với mặt phẳng (P).
Hệ quả 3. Nếu hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng này.
Hệ quả 4. Qua một đường thẳng a không vuông góc với mặt phẳng (P), có một và chỉ có một mặt phẳng (Q) vuông góc với (P).
a không vuông góc với (P)
⇒ ∃!(Q):a⊂(Q)và Q→(P)
– Hiểu khái niệm, tính chất một số hình hộp không gian:
Hình lăng trụ đứng có các cạnh bên vuông góc với đáy;
Hình lăng trụ đều là hình lăng trụ đứng có đáy là một đa giác đều;
Hình hộp đứng là hình lăng trụ đứng có đấy là hình bình hành.
Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật và tất cả các mặt đều là hình chữ nhật.
Hình lập phương là hình hộp chữ nhật có đáy là hình vuông và tất cả các mặt đều là hình vuông.
– Biết khái niệm hình chóp đều và chóp cụt đều:
Hình chóp đều là hình chóp có đáy là đa giác đều và tát cả các cạnh bên bằng nhau và chân đường cao hình chóp là tâm của đa giác đáy.
Hình chóp cụt đều là phần hình chóp đều nằm giữa đáy và một mặt phẳng song song với đáy, cắt tất cả các cạnh bên.
2. Về kĩ năng.
– Xác định được góc giữa hai mặt phẳng
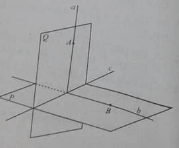
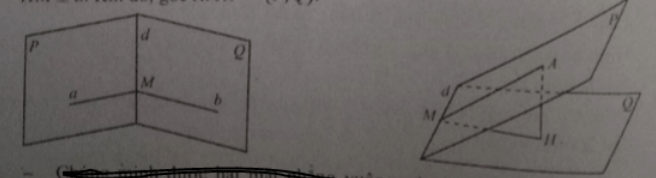
Từ môt điểm M trên giao tuyến d của hai mặt phẳng, vẽ hai đường thẳng a, b lần lượt thuộc hai mặt phẳng và cùng vuông góc với d. góc giữa hai đường thẳng này là góc giữa hai mặt phẳng
Từ điểm A thuộc mặt phẳng (P), vẽ AH vuông góc với mặt phẳng (Q), vẽ HM ⊥ d. khi đó góc
– Chứng minh được hai đường thẳng vuông góc: góc giữa hai mặt phẳng bằng 900; mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
– Vận dụng được tính chất của lẳng trụ đứng, hình hộp. hình chóp đều, chóp cụt đều và giải một số bài tập.
Tham khảo các bài giải Bài tập trắc nghiệm Hình Học 11 khác: