Bài 6. Tính chất của hai tiếp tuyến cắt nhau

A. Lý thuyết về tính chất của hai tiếp tuyến cắt nhau.

Tóm tắt kiến thức:

1. Định lý

Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

– Điểm đó cách đều hai điểm.

– Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

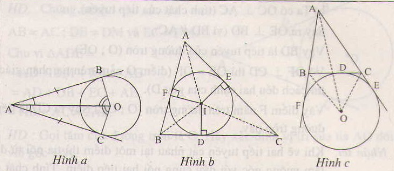
– Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm (h.a).

2. Đường tròn nội tiếp tam giác

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là ngoại tiếp đường tròn.

Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác (h.b).

3. Đường tròn bàng tiếp tam giác

Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.

Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, giao điểm này cùng nằm trên đường phân giác góc A (h.c).

Với một tam giác, có ba đường tròn bàng tiếp. 

B. Bài tập

Bài 26. Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC; biết $OB=2cm,OA=4cm$.

Giải:

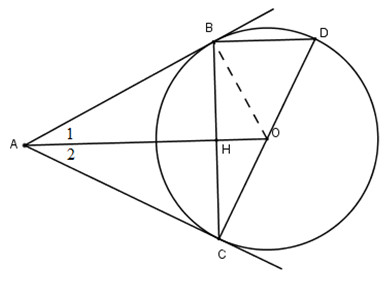
a) Vì AB, AC là các tiếp tuyến nên $AB=AC$ và $\widehat{A_1}=\widehat{A_2}$.

Suy ra $OA\perp BC$ (tính chất của tam giác cân).

b) Điểm B nằm trên đường tròn đường kính CD nên $\widehat{CBD}={90}^{\circ }$.

Suy ra BD//AO (vì cùng vuông góc với BC).

c) Nối OB thì $OB\perp AB.$

Xét tam giác AOB vuông tại B có: $\sin \widehat{A_1}=\frac{O\mathrm{B/}}{OA}=\frac{\mathrm{2/}}{4}=\frac{\mathrm{1/}}{2}$

$\Rightarrow \widehat{A_1}={30}^{\circ }\Rightarrow \widehat{BAC}={60}^{\circ }.$

Tam giác ABC cân, có một góc ${60}^{\circ }$ nên là tam giác đều.

Ta có $A{\mathrm{B^}}^2=O{\mathrm{A^}}^2-O{\mathrm{B^}}^2={\mathrm{4^}}^2-{\mathrm{2^}}^2=12\Rightarrow AB=2\sqrt{3.}$

Vậy $AB=AC=BC=2\sqrt{3}cm$.

Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng ${60}^{\circ }$.

Bài 27. Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn O, nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Hướng dẫn giải:

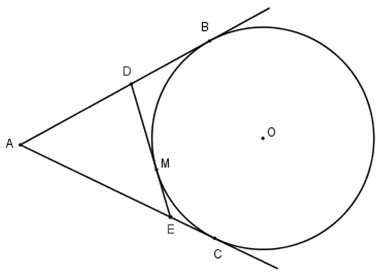
Theo tính chất hai tiếp tuyến cắt nhau ta có;

$AB=AC;DB=DM;EC=EM.$

Chu vi $\Delta ADE=AD+DM+ME+AE$

$=AD+DB+EC+AE$

$=AB+AC=2AB$

Bài 28. Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?

Giải:

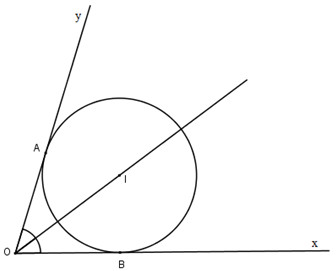
Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:

$\widehat{xAO}=\widehat{yAO}$

Hay AO là tia phân giác của góc xAy. Vậy tâm O các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc(xAy).

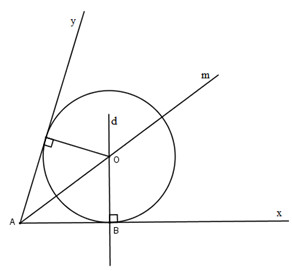
Bài tập 29. Cho góc xAy khác góc bẹt, điểm B thuộc Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.

Giải:

Phân tích 

Đường tròn (O) tiếp xúc với hai cạnh của góc xAy nên tâm O nằm trên tia phân giác Am của góc xAy. Đường tròn (O) tiếp xúc với Ax tại B nên tâm O nằm trên đường thẳng $d\perp Ax$ tại B.

Vậy O là giao điểm của tia Am với đường thẳng d.

Cách dựng

– Dựng tia phân giác Am của góc xAy.

– Qua B dựng đường thẳng $d\perp Ax$, cắt tia Am tại O.

– Dựng đường tròn (O;OB), đó là đường tròn phải dựng.

Chứng minh

Vì $OB\perp Ax$ tại B nên đường tròn (O;OB) tiếp xúc với Ax tại B. 

Vì O nằm trên tia phân giác của góc xAy nên O cách đều hai cạnh của góc xAy. Do đó đường tròn (O;OB) tiếp xúc với Ay.

Biện luận. Bài toán luôn có một nghiệm hình.

Bài 31. Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).

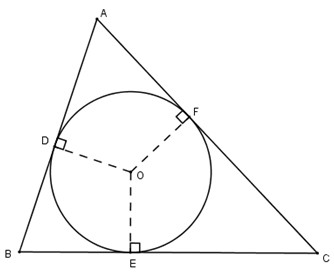
a) Chứng minh rằng:

$2AD=AB+AC-BC.$

b) Tìm các hệ thức tương tự hệ thức ở câu a).

Giải:

a) Theo tính chất của hai tiếp tuyến cắt nhau ta có: 

$AD=AF;BD=BE;CF=CE.$

Xét vế phải:

$AB+AC-BC$

$=(AD+DB)+(AF+FC)-(BE+EC)$

$=AD+AF=2AD.$

b) Các hệ thức tương tự là:

$2BD=BA+BC-AC;$

$2CF=CA+CB-AB.$

Nhận xét. Từ bài toán trên ta có các kết quả sau:

$AD=AF=p-a;$

$BD=BE=p-b$

$CE=CF=p-c$

trong đó $AB=c;BC=a;CA=b$và p là nửa chu vi của tam giác ABC.